Den här artikeln har anpassats från Microsoft Excel Data Analysis and Business Modeling av Wayne L. Winston.
-
Vem använder Monte Carlo-simulering?
-
Vad händer när du skriver =SLUMP() i en cell?
-
Hur kan du simulera värden för en diskret slumpvariabel?
-
Hur kan du simulera värden för en normal slumpvariabel?
-
Hur kan ett hälsningskortsföretag avgöra hur många kort som ska tillverkas?
Vi skulle vilja uppskatta sannolikheterna för osäkra händelser korrekt. Till exempel, vad är sannolikheten för att en ny produkts kassaflöden kommer att ha ett positivt nettonuvärde (NETNUVÄRDE)? Vilken är riskfaktorn för vår investeringsportfölj? Monte Carlo simulering gör det möjligt för oss att modellera situationer som presenterar osäkerhet och sedan spela ut dem på en dator tusentals gånger.
Obs!: Namnet Monte Carlo-simulering kommer från datorsimuleringarna som utfördes under 1930- och 1940-talet för att uppskatta sannolikheten för att kedjereaktionen som behövdes för att en atombomb skulle detonera skulle fungera framgångsrikt. Fysikerna som var involverade i detta arbete var stora fans av spel, så de gav simuleringarna kodnamnet Monte Carlo.
I de kommande fem kapitel, kommer du att se exempel på hur du kan använda Excel för att utföra Monte Carlo simuleringar.
Många företag använder Monte Carlo-simulering som en viktig del av sin beslutsprocess. Här är några exempel.
-
General Motors, Proctor och Gamble, Pfizer, Bristol-Myers Squibb och Eli Lilly använder simulering för att uppskatta både den genomsnittliga avkastningen och riskfaktorn för nya produkter. Hos GM används denna information av VD för att avgöra vilka produkter som kommer till marknaden.
-
GM använder simulering för aktiviteter som att prognostisera nettoinkomsten för företaget, förutsäga strukturella kostnader och inköpskostnader och bestämma dess känslighet för olika typer av risker (såsom ränteförändringar och valutakursfluktuationer).
-
Lilly använder simulering för att fastställa den optimala växtkapaciteten för varje läkemedel.
-
Proctor och Gamble använder simulering för att modellera och optimalt säkra valutarisker.
-
Sears använder simulering för att avgöra hur många enheter av varje produktlinje som ska beställas från leverantörer , till exempel antalet par dockers byxor som ska beställas i år.
-
Olje- och läkemedelsbolag använder simulering för att värdera "verkliga alternativ", till exempel värdet av en option att expandera, kontraktera eller skjuta upp ett projekt.
-
Finansiella planerare använder Monte Carlo simulering för att bestämma optimala investeringsstrategier för sina kunders pensionering.
När du skriver formeln =SLUMP() i en cell får du ett tal som är lika troligt att anta ett värde mellan 0 och 1. Således cirka 25 procent av tiden bör du få ett tal som är mindre än eller lika med 0,25; cirka 10 procent av tiden bör du få ett tal som är minst 0,90 och så vidare. För att visa hur funktionen SLUMP fungerar kan du ta en titt på filen Randdemo.xlsx, som visas i Bild 60-1.
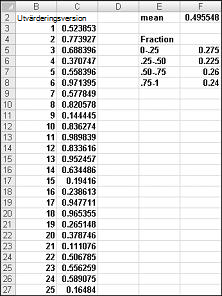
Obs!: När du öppnar filen Randdemo.xlsx visas inte samma slumptal i bild 60–1. Funktionen SLUMP beräknar alltid automatiskt om de tal som genereras när ett kalkylblad öppnas eller när ny information anges i kalkylbladet.
Kopiera först från cell C3 till C4:C402 formeln =SLUMP(). Sedan namnger du området C3:C402 Data. I kolumn F kan du sedan spåra medelvärdet av de 400 slumptalen (cell F2) och använda funktionen ANTAL.OM för att avgöra bråktalen mellan 0 och 0,25, 0,25 och 0,50, 0,50 och 0,75 och 0,75 och 1. När du trycker på F9 beräknas slumptalen om. Observera att medelvärdet av de 400 talen alltid är cirka 0,5 och att cirka 25 procent av resultaten är i intervall om 0,25. Dessa resultat överensstämmer med definitionen av ett slumptal. Observera också att värdena som genereras av SLUMP i olika celler är oberoende. Om det slumptal som genereras i cell C3 till exempel är ett stort tal (t.ex. 0,99) berättar det ingenting om värdena för de andra slumptal som genereras.
Anta att efterfrågan på en kalender styrs av följande diskreta slumpvariabel:
|
Efterfrågan |
Sannolikhet |
|
10 000 |
0,10 |
|
20 000 |
0,35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Hur kan vi låta Excel spela ut, eller simulera, den här efterfrågan på kalendrar många gånger? Tricket är att koppla varje möjligt värde i funktionen SLUMP till ett möjligt behov för kalendrar. Följande tilldelning säkerställer att efterfrågan på 10 000 inträffar 10 procent av tiden och så vidare.
|
Efterfrågan |
Slumpmässigt nummer tilldelat |
|
10 000 |
Mindre än 0,10 |
|
20 000 |
Större än eller lika med 0,10 och mindre än 0,45 |
|
40,000 |
Större än eller lika med 0,45 och mindre än 0,75 |
|
60 000 |
Större än eller lika med 0,75 |
För att visa simuleringen av efterfrågan, titta på filen Discretesim.xlsx, som visas i Bild 60-2 på nästa sida.
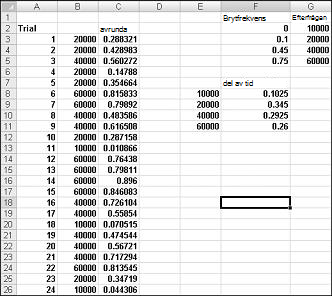
Nyckeln till vår simulering är att använda ett slumptal för att initiera ett uppslag från tabellområdet F2:G5 (namngivet uppslag). Slumptal som är större än eller lika med 0 och mindre än 0,10 ger en efterfrågan på 10 000. slumptal som är större än eller lika med 0,10 och mindre än 0,45 kommer att ge en efterfrågan på 20 000. slumptal som är större än eller lika med 0,45 och mindre än 0,75 kommer att ge en efterfrågan på 40 000. och slumptal som är större än eller lika med 0,75 ger en efterfrågan på 60 000. Du genererar 400 slumptal genom att kopiera formeln SLUMP()från C3 till C4:C402. Sedan genererar du 400 försök, eller iterationer, av kalenderkrav genom att kopiera från B3 till B4:B402 formeln LETARAD(C3,letaupp,2). Den här formeln säkerställer att ett slumptal som är mindre än 0,10 genererar en efterfrågan på 10 000, ett slumpmässigt tal mellan 0,10 och 0,45 genererar en efterfrågan på 20 000 och så vidare. I cellområdet F8:F11 använder du funktionen ANTAL.OM för att avgöra vilken del av våra 400 iterationer som ger varje behov. När vi trycker på F9 för att beräkna om slumptalen ligger de simulerade sannolikheterna nära våra antagna sannolikheter.
Om du skriver formeln NORMINV(rand(),mu,sigma) i en cell genererar du ett simulerat värde för en normal slumpvariabel med ett medelvärde för mu och standardavvikelse sigma. Den här proceduren illustreras i filen Normalsim.xlsx, som visas i Bild 60-3.
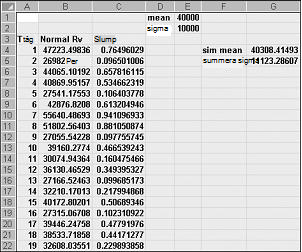
Anta att vi vill simulera 400 försök, eller iterationer, för en normal slumpvariabel med ett medelvärde på 40 000 och en standardavvikelse på 10 000. (Du kan skriva dessa värden i cellerna E1 och E2 och namnge dessa celler som medelvärde respektive sigma.) Om du kopierar formeln =SLUMP() från C4 till C5:C403 genereras 400 olika slumptal. Om du kopierar från B4 till B5:B403 genererar formeln NORMINV(C4,mean,sigma) 400 olika testvärden från en normal slumpvariabel med medelvärdet 40 000 och en standardavvikelse på 10 000. När vi trycker på F9 för att beräkna om slumptalen förblir medelvärdet nära 40 000 och standardavvikelsen nära 10 000.
I grund och botten, för ett slumptal x, genererar formeln NORMINV(p,mu,sigma) den p:te percentilen av en normal slumpvariabel med en medelvärdes mu och ett standardavvikelse sigma. Exempelvis genererar slumptalet 0,77 i cell C4 (se bild 60-3) i cell B4 ungefär den 77:e percentilen av en normal slumpvariabel med medelvärdet 40 000 och en standardavvikelse på 10 000.
I det här avsnittet kommer du att se hur Monte Carlo simulering kan användas som ett beslutsverktyg. Anta att efterfrågan på ett Alla hjärtans dag-kort styrs av följande diskreta slumpvariabel:
|
Efterfrågan |
Sannolikhet |
|
10 000 |
0,10 |
|
20 000 |
0,35 |
|
40,000 |
0,3 |
|
60 000 |
0,25 |
Hälsningskortet säljer för $ 4.00, och den rörliga kostnaden för att producera varje kort är $ 1,50. Överblivna kort måste kasseras till en kostnad av $ 0,20 per kort. Hur många kort ska skrivas ut?
I grund och botten simulerar vi varje möjlig produktionskvantitet (10 000, 20 000, 40 000 eller 60 000) många gånger (till exempel 1 000 iterationer). Sedan bestämmer vi vilken orderantal som ger den maximala genomsnittliga vinsten över de 1000 iterationerna. Du hittar data för det här avsnittet i filen Valentine.xlsx, som visas i Bild 60-4. Du tilldelar områdesnamnen i cellerna B1:B11 till cellerna C1:C11. Cellområdet G3:H6 tilldelas namnuppslag. Våra parametrar för försäljningspris och kostnad anges i cellerna C4:C6.
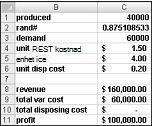
Du kan ange ett antal försöksproduktion (40 000 i det här exemplet) i cell C1. Skapa sedan ett slumptal i cell C2 med formeln =SLUMP(). Som tidigare beskrivits simulerar du efterfrågan på kortet i cell C3 med formeln LETARAD(rand;uppslag;2). (I LETARAD-formeln är slump cellnamnet som tilldelats cell C3, inte funktionen SLUMP.)
Antalet sålda enheter är den mindre av vår produktionsmängd och efterfrågan. I cell C8 beräknar du våra intäkter med formeln MIN(producerad,efterfrågan)*unit_price. I cell C9 beräknar du den totala produktionskostnaden med formeln producerad*unit_prod_cost.
Om vi producerar fler kort än vad som efterfrågas är antalet enheter kvar lika med produktionen minus efterfrågan. annars finns inga enheter kvar. Vi beräknar vår avfallshanteringskostnad i cell C10 med formeln unit_disp_cost*OM(producerad>efterfrågan,producerad–efterfrågan,0). Slutligen, i cell C11, beräknar vi vår vinst som intäkter – total_var_cost-total_disposing_cost.
Vi vill ha ett effektivt sätt att trycka på F9 många gånger (till exempel 1000) för varje produktionsantal och räkna vår förväntade vinst för varje kvantitet. Denna situation är en där en tvåvägsdatatabell kommer till vår räddning. (Mer information om datatabeller finns i Kapitel 15, "Känslighetsanalys med datatabeller".) Datatabellen som används i det här exemplet visas i Bild 60–5.
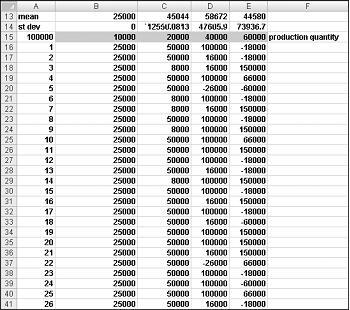
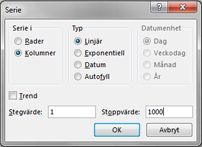
I cellområdet A16:A1015 anger du siffrorna 1–1 000 (motsvarande 1 000 försök). Ett enkelt sätt att skapa dessa värden är att börja med att ange 1 i cell A16. Markera cellen och klicka sedan på Fyllning på fliken Start i gruppen Redigering och välj Serie för att visa dialogrutan Serie. I dialogrutan Serie , som visas i Bild 60–6, anger du stegvärdet 1 och stoppvärdet 1 000. I området Serie i väljer du alternativet Kolumner och klickar sedan på OK. Talen 1–1 000 anges i kolumn A med början i cell A16.
Därefter anger vi våra möjliga produktionsmängder (10 000, 20 000, 40 000, 60 000) i cellerna B15:E15. Vi vill beräkna vinsten för varje försöksnummer (1 till 1 000) och varje produktionsantal. Vi refererar till formeln för vinst (beräknad i cell C11) i den övre vänstra cellen i vår datatabell (A15) genom att ange =C11.
Vi är nu redo att lura Excel att simulera 1 000 iterationer av efterfrågan för varje produktionsantal. Markera tabellområdet (A15:E1014) och klicka sedan på Konsekvensanalys i gruppen Dataverktyg på fliken Data och välj sedan Datatabell. Om du vill skapa en tvåvägsdatatabell väljer du produktionsantalet (cell C1) som radindatacell och väljer en tom cell (vi valde cell I14) som kolumnindatacell. När du har klickat på OK simulerar Excel 1 000 efterfrågevärden för varje orderantal.
Ta hänsyn till värdena i datatabellen i cellområdet C16:C1015 för att förstå varför det fungerar. För var och en av dessa celler använder Excel värdet 20 000 i cell C1. I C16 placeras kolumnindatacellvärdet 1 i en tom cell och slumptalet i cell C2 beräknas om. Motsvarande vinst registreras sedan i cell C16. Sedan placeras kolumncellens indatavärde 2 i en tom cell och slumptalet i C2 beräknas om. Motsvarande vinst anges i cell C17.
Genom att kopiera från cell B13 till C13:E13 formeln MEDEL(B16:B1015) beräknar vi genomsnittlig simulerad vinst för varje produktionsantal. Genom att kopiera från cell B14 till C14:E14 formeln STDAV(B16:B1015) beräknar vi standardavvikelsen för våra simulerade vinster för varje orderantal. Varje gång vi trycker på F9 simuleras 1 000 iterationer av efterfrågan för varje orderantal. Att producera 40 000 kort ger alltid den största förväntade vinsten. Därför verkar det som om det är rätt beslut att producera 40 000 kort.
Riskens inverkan på vårt beslut Om vi producerade 20 000 i stället för 40 000 kort minskade vår förväntade vinst cirka 22 procent, men vår risk (mätt med standardavvikelsen för vinst) sjönk nästan 73 procent. Därför, om vi är extremt motvilliga till risk, kan det vara rätt beslut att producera 20 000 kort. För övrigt producerar 10.000 kort alltid har en standardavvikelse på 0 kort eftersom om vi producerar 10.000 kort, kommer vi alltid att sälja alla utan några rester.
Obs!: I den här arbetsboken är alternativet Beräkning inställt på Automatisk utom tabeller. (Använd kommandot Beräkning i gruppen Beräkning på fliken Formler.) Den här inställningen säkerställer att vår datatabell inte beräknas om om vi inte trycker på F9, vilket är en bra idé eftersom en stor datatabell gör ditt arbete långsammare om den beräknas om varje gång du skriver något i kalkylbladet. Observera att när du trycker på F9 i det här exemplet ändras medelvärdets vinst. Detta inträffar eftersom varje gång du trycker på F9 används en annan sekvens med 1 000 slumptal för att generera krav för varje orderantal.
Konfidensintervall för genomsnittlig vinst En naturlig fråga att ställa i denna situation är, i vilket intervall är vi 95 procent säkra på att den verkliga genomsnittliga vinsten kommer att falla? Det här intervallet kallas konfidensintervallet 95 procent för medelvärdesvinst. Ett konfidensintervall på 95 procent för medelvärdet av simuleringsresultat beräknas med följande formel:
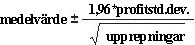
I cell J11 beräknar du den undre gränsen för konfidensintervallet på 95 procent för genomsnittlig vinst när 40 000 kalendrar skapas med formeln D13–1,96*D14/SQRT(1000). I cell J12 beräknar du den övre gränsen för konfidensintervallet på 95 procent med formeln D13+1,96*D14/SQRT(1000). Beräkningarna visas i Bild 60–7.

Vi är 95 procent säkra på att vår genomsnittliga vinst när 40 000 kalendrar beställts är mellan $ 56,687 och $ 62,589.
-
En GMC-återförsäljare tror att efterfrågan på 2005-sändebud normalt kommer att fördelas med ett medelvärde på 200 och standardavvikelsen på 30. Hans kostnad för att ta emot ett sändebud är 25 000 dollar, och han säljer ett sändebud för 40 000 dollar. Hälften av alla sändebud som inte säljs till fullt pris kan säljas för $ 30,000. Han överväger att beordra 200, 220, 240, 260, 280 eller 300 sändebud. Hur många ska han beställa?
-
En liten stormarknad försöker avgöra hur många kopior av Personer tidning de ska beställa varje vecka. De tror att deras efterfrågan på Personer styrs av följande diskreta slumpmässiga variabel:
Efterfrågan
Sannolikhet
15
0,10
20
0.20
25
0.30
30
0,25
35
0,15
-
Snabbköpet betalar $ 1.00 för varje kopia av Personer och säljer den för $ 1.95. Varje osåld kopia kan returneras för $0,50. Hur många kopior av Personer ska store-beställningen vara?
Behöver du mer hjälp?
Du kan alltid fråga en expert i Excel Tech Community eller få support i Communities.










