CONFIDENCE.NORM (funkcija CONFIDENCE.NORM)

Opis

Interval pouzdanosti je opseg vrednosti. Srednja vrednost uzorka, x, nalazi se u centru ovog opsega, a opseg je x ± CONFIDENCE.NORM. Na primer, ako je x srednja vrednost uzorka vremena isporuke za proizvode naručene poštom, x ± CONFIDENCE.NORM je opseg srednjih vrednosti populacije. Za bilo koju srednju vrednost populacije, µ0, u ovom opsegu verovatnoća pribavljanja srednje vrednosti uzorka dalje od µ0x je veća od alfa. Za bilo koju srednju vrednost populacije, µ0, izvan ovog opsega verovatnoća pribavljanja srednje vrednosti uzorka dalje od µ0x je manja od alfa. Drugim rečima, pretpostavimo da koristimo parametre x, standardna_dev i veličina za kreiranje dvosmernog testa na nivou značaja alfa hipoteze da je srednja vrednost populacije µ0. Tu hipotezu nećemo odbaciti ako je µ0 u intervalu pouzdanosti, a odbacićemo je ako µ0 nije u intervalu pouzdanosti. Interval pouzdanosti nam ne dozvoljava da zaključimo da postoji verovatnoća 1 – alfa da će vreme isporuke našeg sledećeg paketa biti u intervalu pouzdanosti.

Sintaksa

CONFIDENCE.NORM(alfa,standardna_dev,veličina)

Sintaksa funkcije CONFIDENCE.NORM ima sledeće argumente:

• Alfa     Obavezno. Nivo značaja koji se koristi za izračunavanje nivoa pouzdanosti. Nivo pouzdanosti jednak je 100*(1 – alfa)%. Drugim rečima, vrednost alfa od 0,05 znači nivo pouzdanosti od 95 procenata.

• Standardna_dev     Obavezno. Standardna devijacija populacije za opseg podataka i pretpostavlja se da je poznata.

• Veličina     Obavezno. Veličina uzorka.

Primedbe

• Ako neki od argumenata nije broj, funkcija CONFIDENCE.NORM vraća vrednost greške #VALUE!.

• Ako je parametar alfa ≤ 0 ili je alfa ≥ 1, funkcija CONFIDENCE.NORM vraća vrednost greške #NUM!.

• Ako je parametar standardna_dev ≤ 0, funkcija CONFIDENCE.NORM vraća vrednost greške #NUM!.

• Ako argument veličina ima decimale, one se odsecaju.

• Ako je parametar veličina < 1, funkcija CONFIDENCE.NORM vraća vrednost greške #NUM!.

• Ako pretpostavimo da je alfa jednako 0,05, treba da izračunamo površinu ispod standardne krive normalne raspodele koja je jednaka (1 – alfa) ili 95 procenata. Ova vrednost je ± 1,96. Dakle, interval pouzdanosti je:

  

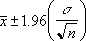
Primer

Kopirajte date primere podataka u sledeću tabelu i nalepite ih u ćeliju A1 novog radnog lista u programu Excel. Ako želite da formule izračunaju rezultate, izaberite formule, pritisnite taster F2, a zatim pritisnite taster Enter. Ako je potrebno, možete prilagoditi širinu kolona kako biste videli sve podatke u njima.