V tem članku je opisana sintaksa formule in uporaba LINEST v Microsoft Excelu. Povezave do več informacij o risanju grafikonov in izvajanju regresivne analize so v razdelku Glejte tudi.
Opis
Funkcija LINESTizračuna statistiko za premico, in sicer z načinom »najmanjših kvadratov« izračuna premico, ki vašim podatkom najbolj ustreza, in vrne matriko, ki opisuje premico. Funkcijo LINEST lahko združite tudi z drugimi funkcijami in izračunate statistiko drugih vrst modelov, ki so linearni v neznanih parametrih, vključno s polinomskimi, logaritmičnimi, eksponentnimi in naraščajočimi nizi. Funkcija vrne matriko vrednosti, zato mora biti v obliki matrične formule. Navodila se nanašajo na primere v tem članku.
Enačba premice je:
y = mx + b
–ali–
y = m1x1 + m2x2 +... + b
če obstaja več obsegov vrednosti x, kjer so odvisne vrednosti y funkcija neodvisnih x-vrednosti. Vrednosti m so koeficienti, ki ustrezajo vsaki x-vrednosti, b pa je konstantna vrednost. Vedite, da so y, x in m lahko tudi vektorji. Matrika, ki jo vrne funkcija LINEST , je {mn,mn-1,...,m1,b}. LINEST lahko vrne tudi dodatno regresijsko statistiko.
Sintaksa
LINEST(znani_y-i, [znani_x-i], [konstanta], [statistika])
V sintaksi funkcije LINEST so ti argumenti:
Sintaksa
-
znani_y-i Obvezen. Nabor vrednosti y, ki jih že poznate v razmerju y = mx + b.
-
Če je obseg znani_y-i v enem stolpcu, je vsak stolpec argumenta znani_x-i obravnavan kot ločena spremenljivka.
-
Če je obseg argumenta znani_y-i v eni vrstici, je vsaka vrstica argumenta znani_x-i obravnavana kot ločena spremenljivka.
-
-
znani_x-i Neobvezen. Nabor vrednosti x, ki jih morda že poznate v razmerju y = mx + b.
-
Obseg znani_x-i lahko vsebuje enega ali več naborov spremenljivk. Če uporabite samo eno spremenljivko, sta lahko argumenta znani_y-i in znani_x-i obsega poljubne oblike, imeti morata le enake mere. Če pa uporabljate več spremenljivk, mora biti argument znani_y-i vektor (torej obseg z višino ene vrstice in širino enega stolpca).
-
Če argument znani_x-i izpustite, privzame program zanj vrednost matrike {1;2;3;...}, ki je iste velikosti kot argument znani_y-i.
-
-
konstanta Neobvezen. Logična vrednost, ki navaja, ali naj bo konstanta b enaka 0.
-
Če je argument konstanta enak TRUE ali če ga izpustite, je b izračunan normalno.
-
Če je konstanta FALSE, je b enak 0 in vrednost m se prilagodijo tako, da ustrezajo y = mx.
-
-
statistika Neobvezen. Logična vrednost, ki določa, ali naj funkcija vrne dodatno regresijsko statistiko.
-
Če je argument »statistika « TRUE, vrne LINEST dodatno regresijsko statistiko; posledično je vrnjena matrika {mn,mn-1,...,m1,b; sen,sen-1,...,se1,seb; r2,sey; F; df; ssreg, ssresid}.
-
Če je argument statistika FALSE ali izpuščen, LINEST vrne le koeficiente m in konstanto.
Dodatne regresivne statistike so:
-
|
Statistika |
Opis |
|---|---|
|
se1,se2,...,sen |
Standardne vrednosti napak za koeficiente m1,m2,...,mn. |
|
seb |
Standardne vrednosti napak za konstanto b (seb = #N/V, kadar je argument konstanta FALSE). |
|
r2 |
Koeficient določnosti. Primerja ocenjene in dejanske vrednosti y in jih razvrsti od 0 do 1. Če je 1, obstaja v vzorcu popolna korelacija – med ocenjeno in dejansko vrednostjo y ni razlik. V drugi skrajnosti, če je koeficient določnosti enak 0, vam regresivna enačba pri predvidevanju vrednosti y ne pomaga. Če želite več informacij otem, kako se izračuna 2, glejte »Opombe« v nadaljevanju te teme. |
|
sey |
Standardna napako z vrednostjo za y ocene. |
|
F |
F statistika, ali F-opazovana vrednost. F statistiko uporabite, če želite ugotoviti ali se opazovana zveza med odvisno in neodvisno spremenljivko pojavi slučajno. |
|
df |
Stopnje prostosti. Z stopnjami prostosti lahko poiščete F-kritične vrednosti v statistični tabeli. Primerjajte vrednosti v tabeli s statistiko F, ki jo vrne LINEST , da določite raven zaupanja za model. Če želite več informacij o tem, kako se izračuna df, glejte »Opombe« v nadaljevanju te teme. 4 . primer prikazuje uporabo F in df. |
|
ssreg |
Regresivna vsota kvadratov. |
|
ssresid |
Vsota ostankov kvadratov. Če želite več informacij o tem, kako se izračunata ssreg in ssresid, glejte »Opombe« v nadaljevanju te teme. |
Naslednji primer ilustrira vrstni red v katerem se dodatne regresivne statistike vrnejo.

Opombe
-
Vsako premico lahko opišete z naklonom in y-presečišči:
Naklon (m):
Če želite poiskati naklon črte, pogosto napisane kot m, vzemite dve točki na črti (x1,y1) in (x2,y2); naklon je enak (y2 - y1)/(x2 - x1).Y-presečišče (b):
Y-presečišče črte, pogosto napisano kot b, je vrednost y v točki, kjer črta seka os y.Enačba ravne črte je y = mx + b. Ko poznate vrednosti m in b, lahko izračunate katero koli točko v vrstici tako, da v enačbo priključite y ali x. Uporabite lahko tudi funkcijo TREND .
-
Kadar imate le eno neodvisno vrednost spremenljivke x, lahko naklon in presečišče neposredno s temi formulami:
Pobočju:
=INDEX(LINEST(known_y; known_x; 1)Y-presečišče:
=INDEX(LINEST(known_y; known_x); 2) -
Natančnost premice, izračunane z LINEST je odvisna od stopnje raztresenosti podatkov. Bolj kot so podatki linearni, bolj točen je model funkcije LINEST. Funkcija LINEST za določanje najboljšega ujemanja s podatki uporablja način najmanjših kvadratov. Kadar imate le eno neodvisno spremenljivko x, izračun za m in b temelji na teh formulah:
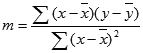
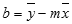
pri čemer sta x in y vzorčni srednji vrednosti; tj. x = AVERAGE(znani_x-i) in y = AVERAGE(znani_y-i).
-
Funkciji line- in curve-fitting LINEST in LOGEST lahko izračunata najboljšo ravno črto ali eksponentno krivuljo, ki ustreza vašim podatkov. Vendar pa se morate odločiti, kateri od obeh rezultatov najbolje ustreza vašim podatkovom. TREND(e known_y,known_x) lahko izračunate za ravno črto ali GROWTH(known_y-e, known_x-e) za eksponentno krivuljo. Te funkcije brez argumenta new_x vrne matriko vrednosti y, napovedanih vzdolž te črte ali krivulje v dejanskih podatkovnih točkah. Nato lahko primerjate predvidene vrednosti z dejanskimi vrednostmi. Morda boste želeli obe grafikoni ustvariti v obliki grafikona za vizualno primerjavo.
-
V regresijski analizi Excel za vsako točko izračuna kvadratno razliko med y-vrednostjo, ocenjeno za to točko in dejansko vrednostjo y. Vsota teh kvadratnih razlik se imenuje vsota ostankov kvadratov, ssresid. Excel nato izračuna skupno vsoto kvadratov, sstotal. Če je argument konstanta = TRUE ali je izpuščen, je skupna vsota kvadratov vsota kvadratnih razlik med dejanskimi vrednostmi y in povprečjem y-vrednosti. Ko je argument » konstanta« = FALSE, je skupna vsota kvadratov vsota kvadratov dejanskih y-vrednosti (brez odštevanja povprečne vrednosti y od vsake posamezne y-vrednosti). Nato regresijsko vsoto kvadratov, ssreg, je mogoče najti iz: ssreg = sstotal - ssresid. Manjša kot je vsota ostankov kvadratov, v primerjavi s skupno vsoto kvadratov, večja je vrednost koeficienta določne vrednosti r2, ki je kazalnik, kako dobro enačba, ki je posledica regresijske analize, pojasnjuje razmerje med spremenljivkami. Vrednost r2 je enaka ssreg/sstotal.
-
V nekaterih primerih eden ali več stolpcev X (recimo, da sta stolpca Y in X) morda nima dodatne napovedne vrednosti v prisotnosti drugih stolpcev X. Z drugimi besedami, če odstranite enega ali več stolpcev X, boste morda vodili do enako točnih predvidenih vrednosti Y. V tem primeru morate te odvečne stolpce X izpustiti iz regresivnega modela. Ta pojav se imenuje kolinearnost, ker lahko kateri koli odvečni stolpec X izrazite kot vsoto večkratnikov ne redundantnih stolpcev X. Funkcija LINEST preveri kolinearnost in odstrani odvečne stolpce X iz regresivnega modela, ko jih prepozna. Odstranjene stolpce X je v linestu mogoče prepoznati kot koeficiente 0 poleg vrednosti 0 se. Če odstranite enega ali več stolpcev kot odvečnih, to vpliva na df, ker je df odvisen od števila stolpcev X, ki se dejansko uporabljajo za predvidevanje. Če želite podrobnosti o izračunu df, glejte 4. primer. Če se vrednost df spremeni, ker so odstranjeni odvečni stolpci X, vplivate tudi na vrednosti sey in F. Kolinearnost mora biti v praksi razmeroma redka. Vendar pa je bolj verjetno, da bo prišlo do tega, če nekateri stolpci X vsebujejo le vrednosti 0 in 1 kot indikator, ali je predmet v preskusu ali ne član določene skupine. Če je argument konstanta = TRUE ali je izpuščen, funkcija LINEST učinkovito vstavi dodatni stolpec X vseh vrednosti 1 za modeliranje presečišče. Če imate stolpec z 1 za vsak predmet, če je moški, ali 0, če ni, in imate tudi stolpec z 1 za vsak predmet, če je ženski, ali 0, če ni, je ta zadnji stolpec odveč, ker je vnose v njem mogoče dobiti odštte iz vnosa v stolpcu »moški indikator« od vnosa v dodatni stolpec vseh 1 vrednosti, dodanih s funkcijo LINEST .
-
Ko iz modela zaradi kolinearnosti ni odstranjen noben stolpec, vrednost df izračunamo tako: če imamo k stolpcev z vrednostmi znani_x-i in je argument konstanta = TRUE ali je izpuščen, potem velja: df = n – k – 1. Če je argument konstanta = FALSE, potem velja: df = n - k. V obeh primerih pa se za vsak stolpec X, ki je bil odstranjen zaradi kolinearnosti, vrednost df poveča za 1.
-
Kadar matrično konstanto (kot je znani_x-i) vnašate kot argument, s podpičji ločite vrednosti v isti vrstici in s poševnicami nazaj ločite posamezne vrstice. Ločilni znaki so lahko tudi drugi, odvisno od področnih nastavitev.
-
Bodite pozorni na to, da vrednosti y, predvidene z regresivno analizo, morda niso veljavne, če so zunaj obsega y vrednosti, ki ste jih uporabili za določanje enačbe.
-
Temeljni algoritem, ki se uporablja v funkciji LINEST, je drugačen od temeljnega algoritma, ki se uporablja v funkcijah SLOPE in INTERCEPT. Razlika med tema algoritmoma lahko vodi do različnih rezultatov, ko so podatki nedoločeni in kolinearni. Če so na primer podatkovne točke argumenta znani_y-i 0 in podatkovne točke argumenta znani_x-i 1:
-
LINEST vrne vrednost 0. Algoritem funkcije LINEST je oblikovan tako, da vrne stvarne rezultate za kolinearne podatke in v tem primeru je mogoče poiskati vsaj en odgovor.
-
SLOPE in INTERCEPT vrneta #DIV/0! napaka #REF!. Algoritem funkcij SLOPE in INTERCEPT je zasnovan tako, da poišče le en odgovor in v tem primeru je lahko odgovor več.
-
-
Poleg tega, da lahko s funkcijo LOGEST izračunate statistiko za druge regresijske vrste, lahko s funkcijo LINEST izračunate obseg drugih regresijskih vrst tako, da vnesete funkcije spremenljivk X in Y kot niza X in Y za LINEST. Na primer ta formula:
=LINEST(yvrednosti; xvrednosti^COLUMN($A:$C))
Deluje, ko imate en stolpec z vrednostmi Y in en stolpec z vrednostmi X za izračun kvadratnega (polinomski vrstnega reda 3) približka oblike:
y = m1*x + m2*x^2 + m3*x^3 + b
To formulo lahko prilagodite za izračun drugih vrst regresije, vendar v nekaterih primerih to zahteva prilagoditev izhodnih vrednosti in drugih statistik.
-
Vrednost F-tesat, ki jo vrne funkcija LINEST, se razlikuje od vrednosti F-testa, ki jo vrne funkcija FTEST. LINEST vrne F-statistiko, medtem ko FTEST vrne verjetnost.
Primeri
1. primer – Naklon in y-presečišče
Kopirajte vzorčne podatke iz te tabele in jih prilepite v celico A1 v novem Excelovem delovnem listu. Če želite, da formule prikažejo rezultate, jih izberite, pritisnite F2 in nato tipko ENTER. Po potrebi lahko prilagodite širine stolpcev in si ogledate vse podatke.
|
Znani y |
Znani x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Rezultat (naklon) |
Rezultat (presečišče z y) |
|
2 |
1 |
|
Formula (formula s polji v celicah A7:B7) |
|
|
=LINEST(A2:A5,B2:B5,,FALSE) |
2. primer – Preprosta linearna regresija
Kopirajte vzorčne podatke iz te tabele in jih prilepite v celico A1 v novem Excelovem delovnem listu. Če želite, da formule prikažejo rezultate, jih izberite, pritisnite F2 in nato tipko ENTER. Po potrebi lahko prilagodite širine stolpcev in si ogledate vse podatke.
|
Mesec |
Prodaja |
|---|---|
|
1 |
$ 3.100 |
|
2 |
$ 4.500 |
|
3 |
$ 4.400 |
|
4 |
$ 5.400 |
|
5 |
$ 7.500 |
|
6 |
$ 8.100 |
|
Formula |
Rezultat |
|
=SUM(LINEST(B1:B6, A1:A6)*{9,1}) |
11.000 € |
|
Izračuna oceno prodaje v devetem mesecu, ki temelji na prodaji od 1. do 6. meseca. |
3. primer – Večkratna linearna regresija
Kopirajte vzorčne podatke iz te tabele in jih prilepite v celico A1 v novem Excelovem delovnem listu. Če želite, da formule prikažejo rezultate, jih izberite, pritisnite F2 in nato tipko ENTER. Po potrebi lahko prilagodite širine stolpcev in si ogledate vse podatke.
|
Površina tal (x1) |
Pisarne (x2) |
Vhodi (x3) |
Starost (x4) |
Ocenjena vrednost (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142.000 € |
|
2333 |
2 |
2 |
12 |
144.000 € |
|
2356 |
3 |
1,5 |
33 |
151.000 € |
|
2379 |
3 |
2 |
43 |
150.000 € |
|
2402 |
2 |
3 |
53 |
139.000 € |
|
2425 |
4 |
2 |
23 |
169.000 € |
|
2448 |
2 |
1,5 |
99 |
126.000 € |
|
2471 |
2 |
2 |
34 |
142.900 € |
|
2494 |
3 |
3 |
23 |
163.000 € |
|
2517 |
4 |
4 |
55 |
169.000 € |
|
2540 |
2 |
3 |
22 |
149.000 € |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Formula (dinamična formula polja, vnesena v A19) |
||||
|
=LINEST(E2:E12,A2:D12,TRUE,TRUE) |
4. primer – uporaba statistik F in r2
V prejšnjem primeru je bil dejavni koeficient ali r2 0,99675 (glejte celico A17 v rezultatu funkcije LINEST), kar kaže na močno razmerje med neodvisnimi spremenljivkami in prodajno ceno. Če želite ugotoviti, ali so se rezultati tako visoke vrednosti r2 pojavili po naključju, uporabite statistiko F.
Za trenutek si zamislite, da odnos med spremenljivkami sploh ne obstaja, ampak da ste izbrali redek vzorec 11 poslovnih prostorov, kar je povzročilo, da statistične analize prikazujejo močan odnos. Izraz »alfa« se uporablja za verjetnost zmotnih zaključkov, da odnos obstaja.
Vrednosti F in df v rezultatu funkcije LINEST je mogoče uporabiti za oceno verjetnosti, da se bo po naključju pojavila višja vrednost F. F lahko primerjate s kritičnimi vrednostmi v objavljenih tabelah F-porazdelitve ali s funkcijo FDIST v Excelu, če želite izračunati verjetnost, da se bo po naključju pojavila večja F-vrednost. Ustrezna porazdelitev F ima prostostni stopnji v1 in v2. Če je n število podatkovnih točk in je konstanta = TRUE ali izpuščeno, potem velja v1 = n – df – 1 in v2 = df. (Če je argument konstanta = FALSE, potem je v1 = n – df in v2 = df.) Funkcija FDIST – s sintakso FDIST(F; v1; v2) – bo vrnila verjetnost, da se bo po naključju pojavila višja vrednost F. V tem primeru je df = 6 (celica B18) in F = 459,753674 (celica A18).
Če privzamemo vrednost argumenta »alfa« 0,05, v1 = 11 – 6 – 1 = 4 in v2 = 6, je kritična raven F enaka 4,53. Ker je vrednost F = 459,753674 veliko večja od 4,53, je zelo malo verjetno, da se je tako visoka vrednost F pojavila naključno. (Pri vrednosti argumenta »alfa« = 0,05 moramo hipotezo, da med argumentoma znani_y-i in znani_x-i ni povezave, zavrniti, ko F preseže kritično raven 4,53). Z Excelovo funkcije FDIST lahko izračunate verjetnost, da se je tako visoka vrednost F pojavila naključno. Na primer FDIST(459,753674; 4; 6) = 1,37E-7 pokaže zelo majhno verjetnost. Če najdete kritično raven F v tabeli ali če jo izračunate z Excelovo funkcijo FDIST, lahko ugotovite, da je regresijska enačba uporabna za napovedovanje ocenjenih vrednosti pisarniških zgradb na tem območju. Zapomnite si, da je zelo pomembno, da uporabite pravilne vrednosti v1 in v2, ki ste jih izračunali v prejšnjem odstavku.
5. primer – Izračun statistike t
Drugi preskus hipoteze bo določil, ali je vsak koeficient naklona uporaben pri oceni ocenjene vrednosti stavbe pisarne v 3. primeru. Če želite na primer preskusiti starostni koeficient za statistično pomembnost, delite -234,24 (koeficient naklona starosti) s 13,268 (ocenjena standardna napaka koeficientov starosti v celici A15). Opazovana vrednost t je:
t = m4 ÷ se4 =-234.24 ÷ 13,268 =-17.7
Če je absolutna vrednost t dovolj visoka, se lahko sklene, da je koeficient naklona uporaben pri oceni ocenjene vrednosti pisarne v 3. primeru. V spodnji tabeli so prikazane absolutne vrednosti 4 opazovanih vrednosti t.
Če si ogledate tabelo v statističnem priročniku, boste ugotovili, da je dvorepa kritična vrednost t s stopnjo prostosti 6 in argumentom »alfa« = 0,05 enaka 2,447. To kritično vrednost lahko dobite tudi z Excelovo funkcijo TINV. TINV(0,05; 6) = 2,447. Ker je absolutna vrednost t (17,7) večja od 2,447, je starost pomembna spremenljivka, kadar ocenjujete ocenjeno vrednost poslovnega prostora. Statistično pomembnost drugih neodvisnih spremenljivk lahko preskusite na podoben način. V nadaljevanju so opazovane vrednosti t za vsako neodvisno spremenljivko.
|
Spremenljivka |
opazovana vrednost t |
|---|---|
|
Kvadratura |
5,1 |
|
Število pisarn |
31,3 |
|
Število vhodov |
4,8 |
|
Starost |
17,7 |
Absolutne vrednosti teh spremenljivk so vse večje od 2,447; zaradi tega so vse spremenljivke, uporabljene v regresivni enačbi, uporabne za napoved ocenjene vrednosti poslovnih prostorov v predelu.










