Если вам нужно разработать сложный статистический или инженерный анализ, можно сэкономить шаги и время с помощью средства анализа. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные макро-функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку "Пакет анализа".
-
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
-
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
-
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
-
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
-
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
-
Примечание: Чтобы включить функции Visual Basic для приложений (VBA) для средства анализаПакет анализа, можно загрузить надстройку Analysis ToolPak — VBA так же, как и средство анализа. В поле Доступные надстройки выберите поле Инструмент анализаПакет — VBA проверка.
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Это средство выполняет простой анализ дисперсии данных для двух или более выборок. Анализ позволяет проверить гипотезу о том, что каждая выборка извлекается из одного базового распределения вероятностей и альтернативной гипотезы о том, что базовые распределения вероятностей не одинаковы для всех выборок. Если есть только два примера, можно использовать функцию листа T.ТЕСТ. При использовании более двух выборок нет удобного обобщения T.Вместо этого можно использовать test и модель Anova Single Factor.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
-
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
-
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).
Функции листа CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, когда измерения каждой переменной наблюдаются для каждого из N субъектов. (Любое отсутствие наблюдения для любого субъекта приводит к тому, что этот объект будет игнорироваться при анализе.) Инструмент корреляционного анализа особенно полезен, если для каждого из N субъектов имеется более двух переменных измерения. Она предоставляет выходную таблицу, матрицу корреляции, которая показывает значение CORREL (или PEARSON), примененное к каждой возможной паре переменных измерения.
Коэффициент корреляции, как и ковариация, является мерой степени, в которой две переменные измерения "изменяются вместе". В отличие от ковариации коэффициент корреляции масштабируется таким образом, что его значение не зависит от единиц измерения, в которых выражены две переменные измерения. (Например, если двумя переменными измерения являются вес и высота, значение коэффициента корреляции не изменяется, если вес преобразуется из фунтов в килограммы.) Значение любого коэффициента корреляции должно находиться в диапазоне от -1 до +1 включительно.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и ковариации можно использовать в одном и том же параметре при наличии N различных переменных измерения, наблюдаемых на наборе лиц. Каждый из инструментов корреляции и ковариации предоставляет выходную таблицу, матрицу, которая показывает коэффициент корреляции или ковариацию соответственно между каждой парой переменных измерения. Разница заключается в том, что коэффициенты корреляции масштабируются в диапазоне от -1 до +1 включительно. Соответствующие ковариации не масштабируются. Коэффициент корреляции и ковариация — это меры степени, в которой две переменные "меняются вместе".
Средство ковариации вычисляет значение функции листа COVARIANCE. P для каждой пары переменных измерения. (Прямое использование COVARIANCE. P, а не средство ковариации является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись по диагонали выходной таблицы средства ковариации в строке i, столбец i является ковариантной i-й переменной измерения с самим собой. Это всего лишь дисперсии численности для этой переменной, вычисленная с помощью функции листа VAR.P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа "Описательная статистика" применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа "Экспоненциальное сглаживание" применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
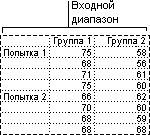
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, "P(F <= f) одностороннее" дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости "Альфа". Если f > 1, "P(F <= f) одностороннее" дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для "Альфа".
Инструмент "Анализ Фурье" применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент "Гистограмма" применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа "Скользящее среднее" применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
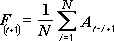
где
-
N — число предшествующих периодов, входящих в скользящее среднее;
-
A j — фактическое значение в момент времени j;
-
F j — прогнозируемое значение в момент времени j.
Инструмент "Генерация случайных чисел" применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Средство анализа ранга и процентиля создает таблицу, содержащую порядковый номер и процентный ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. Это средство использует функции листа RANK. EQ иPERCENTRANK. INC. Если вы хотите учесть связанные значения, используйте RANK. Функция EQ , которая обрабатывает связанные значения как имеющие одинаковый ранг, или использует RANK.Функция AVG, которая возвращает средний ранг для связанных значений.
Инструмент анализа "Регрессия" применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
Средство регрессии использует функцию листа LINEST.
Инструмент анализа "Выборка" создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как "t-статистика" в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 "P(T <= t) одностороннее" дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 "P(T <= t) одностороннее" делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. "t критическое одностороннее" дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного "t критическое одностороннее" равно "Альфа".
"P(T <= t) двустороннее" дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. "P критическое двустороннее" выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем "P критическое двустороннее", равно "Альфа".
Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
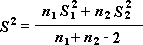
Двухвыборочный t-тест с одинаковыми дисперсиями
Это средство анализа выполняет t-Test учащегося с двумя образцами. В этой форме t-Test предполагается, что два набора данных получены из распределений с одинаковыми отклонениями. Он называется гомоскедастической T-Тест. Этот T-тест можно использовать, чтобы определить, были ли эти две выборки, скорее всего, получены из распределений с равными значениями совокупности.
Двухвыборочный t-тест с различными дисперсиями
Это средство анализа выполняет t-Test учащегося с двумя образцами. В этой форме t-Test предполагается, что два набора данных получены из распределений с неравными отклонениями. Он называется гетероскедасическим t-тестом. Как и в случае с предыдущим вариантом равных отклонений, этот T-тест можно использовать для определения того, были ли две выборки, скорее всего, получены из распределений с равными значениями совокупности. Используйте этот тест, если в двух примерах есть разные субъекты. Используйте парный тест, описанный в следующем примере, если существует один набор испытуемых и две выборки представляют собой измерения для каждого субъекта до и после лечения.
Для определения тестовой величины t используется следующая формула.
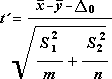
Следующая формула используется для вычисления степеней свободы, df. Так как результат вычисления обычно не является целым числом, значение df округляется до ближайшего целого числа, чтобы получить критическое значение из таблицы t. Функция листа Excel T.ТЕСТ использует вычисляемое значение df без округления, так как можно вычислить значение для T.TEST с неинтечисленным df. Из-за этих различных подходов к определению степеней свободы, результаты Т.ТЕСТ и это средство T-Test будут отличаться в случае неравных отклонений.
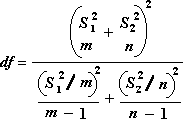
Средство анализа z-Test: Two Sample for Means выполняет два примера z-Test для средств с известными отклонениями. Этот инструмент используется для проверки нулевой гипотезы о том, что между двумя демографическими средствами нет различий в отношении односторонних или двусторонних альтернативных гипотез. Если отклонения не известны, функция листа Z.Вместо этого следует использовать TEST.
При использовании этого инструмента следует внимательно просматривать результат. "P(Z <= z) одностороннее" на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. "P(Z <= z) двустороннее" на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент "z-тест" можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.
Дополнительные сведения
Вы всегда можете задать вопрос эксперту в Excel Tech Community или получить поддержку в сообществах.
См. также
Создание гистограммы в Excel 2016
Создание диаграммы Парето в Excel 2016
Загрузка средства анализаПакет в Excel
Инженерные функции (справочник)
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул










