Ten artykuł zawiera opis składni formuły i zastosowania funkcji REGLINP w programie Microsoft Excel. Aby uzyskać więcej informacji na temat wykresów i wykonywania analizy regresji, skorzystaj z linków dostępnych w sekcji Zobacz też.
Opis
Funkcja REGLINP oblicza statystyki dla linii przy użyciu metody "najmniejszych kwadratów", aby obliczyć linię prostą najlepiej pasjącą do danych, a następnie zwraca tablicę opisującą linię. Funkcję REGLINP można również połączyć z innymi funkcjami, aby obliczyć statystyki dla innych typów modeli liniowych w nieznanych parametrach, takich jak wielomianowe, logarytmiczne, wykładnicze i szeregi potęgowe. Funkcja zwraca tablicę wartości, musi więc być wprowadzana w postaci formuły tablicowej. Instrukcje są zgodne z przykładami w tym artykule.
Równanie dla linii jest następujące:
y = mx + b
— lub —
y = m1x1 + m2x2 + ... + b
jeśli istnieje wiele zakresów wartości x, gdzie zależne wartości y są funkcją niezależnych wartości x. Wartości m to współczynniki odpowiadające każdej wartości zmiennej x, a wartość b jest wartością stałą. Należy zauważyć, że wartości y, x i m mogą być wektorami. Funkcja REGLINP zwraca tablicę {mn;mn-1;...;m1;b}. Funkcja REGLINP może również zwracać dodatkową statystykę regresji.
Składnia
REGLINP(znane_y;[znane_x];[stała];[statystyka])
W składni funkcji REGLINP występują następujące argumenty:
Składnia
-
znane_y Argument wymagany. Jest to zestaw znanych wartości y spełniających zależność y = mx + b.
-
Jeśli zakres znane_y znajduje się w jednej kolumnie, to każda kolumna znane_x jest interpretowana jako oddzielna zmienna.
-
Jeśli zakres znane_y znajduje się w jednym wierszu, to każdy wiersz znane_x jest interpretowany jako oddzielna zmienna.
-
-
znane_x Argument opcjonalny. Jest to zestaw znanych wartości x spełniających zależność y = mx + b.
-
Zakres known_x może zawierać co najmniej jeden zestaw zmiennych. Jeśli jest używana tylko jedna zmienna, known_y i known_x mogą być zakresami dowolnego kształtu, o ile mają jednakowe wymiary. Jeśli jest używana więcej niż jedna zmienna, known_y musi być wektorem (czyli zakresem o wysokości jednego wiersza lub szerokości jednej kolumny).
-
Jeśli argument znane_x jest pominięty, przyjmuje się, że jest on tablicą {1;2;3;...} o takim samym rozmiarze co znane_y.
-
-
stała Argument opcjonalny. Wartość logiczna określająca, czy stała b ma być wymuszana jako równa 0.
-
Jeśli stała ma wartość PRAWDA lub jest pominięta, to stała b jest obliczana normalnie.
-
Jeśli stała ma wartość FAŁSZ, to stała b jest ustawiana jako równa 0, a wartości m są dostosowywane tak, aby wypełnić równanie y = mx.
-
-
statystyka Argument opcjonalny. Wartość logiczna określająca, czy mają być zwracane dodatkowe statystyki regresji.
-
Jeśli statystyka ma wartość PRAWDA, funkcja REGLINP zwraca dodatkowe statystyki regresji. w wyniku tego zwrócona tablica to {mn;mn-1,...,m1;b; sen, sen-1,...,se1, seb; r2, sey; F,df; ssreg, ssresid}.
-
Jeśli argument statystyka ma wartość FAŁSZ lub jest pominięty, to funkcja REGLINP zwraca tylko współczynniki m i stałą b.
Poniżej przedstawiono dodatkowe statystyki regresji:
-
|
Statystyka |
Opis |
|---|---|
|
se1;se2;...;sen |
Standardowe wartości błędu dla współczynników m1;m2;...;mn. |
|
seb |
Standardowe wartości błędu dla stałej b (seb = #N/D!, kiedy stała ma wartość FAŁSZ). |
|
r2 |
Współczynnik oznaczania. Umożliwia porównanie szacowanych i rzeczywistych wartości y oraz zakresów wartości z zakresu od 0 do 1. Jeśli jest to 1, w próbce występuje doskonała korelacja — nie ma różnicy między szacowaną wartością y a rzeczywistą wartością y. Na drugim skraju, jeśli współczynnik oznaczania wynosi 0, równanie regresji nie jest pomocne w przewidywaniu wartości y. Aby uzyskać informacje na temat sposobu obliczaniawartości 2 , zobacz sekcję "Uwagi" w dalszej części tego tematu. |
|
sey |
Standardowy błąd oceny y. |
|
F |
Statystyka F lub wartość obserwowana F. Statystyka F służy do określania, czy obserwowana relacja między zmiennymi zależnymi i niezależnymi występuje przypadkowo. |
|
df |
Stopnie swobody. Można użyć stopni swobody, aby łatwiej znaleźć wartości krytyczne F w tabeli statystycznej. Należy porównać wartości znalezione w tabeli ze statystyką F zwróconą przez funkcję REGLINP w celu określenia poziomu ufności modelu. Aby uzyskać informacje o sposobie obliczania wartości df, zobacz sekcję „Spostrzeżenia" w dalszej części tego tematu. W przykładzie 4 opisano sposób korzystania ze statystyki F i wartości df. |
|
ssreg |
Regresyjna suma kwadratów. |
|
ssresid |
Resztkowa suma kwadratów. Aby uzyskać informacje o sposobie obliczania wartości ssreg i ssresid, zobacz sekcję „Spostrzeżenia” w dalszej części tego tematu. |
Na poniższej ilustracji pokazano kolejność zwracania dodatkowych statystyk regresji.

Spostrzeżenia
-
Można opisać dowolną nachyloną linię prostą przecinającą oś y:
Nachylenie (m):
Aby znaleźć nachylenie linii, często pisane jako m, weź dwa punkty na linii (x1,y1) i (x2,y2); nachylenie jest równe (y2 - y1)/(x2 - x1).Przecięcie Y (b):
Przecięcie y linii, często pisane jako b, jest wartością y w punkcie, w którym linia przecina oś y.Równanie linii prostej to y = mx + b. Jeśli znane są wartości m i b, można obliczyć każdy punkt na linii, wstawiając wartość x lub y do tego równania. Można również użyć funkcji REGLINW.
-
Jeżeli istnieje tylko jedna zmienna niezależna x, to można otrzymać nachylenie i punkt przecięcia z osią y bezpośrednio, stosując następujące formuły:
Nachylenie:
=INDEKS(REGLINP(known_y;known_x);1)Przecięcie Y:
=INDEKS(REGLINP(known_y;known_x);2) -
Dokładność linii obliczonej za pomocą funkcji REGLINP zależy od stopnia rozproszenia danych. Im bardziej liniowe są dane, tym dokładniejszy jest model tworzony przez funkcję REGLINP. Funkcja REGLINP korzysta z metody najmniejszych kwadratów, aby określić optymalne dopasowanie danych. Jeśli istnieje tylko jedna zmienna niezależna x, to obliczenia m i b są oparte na następujących formułach:
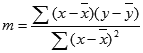
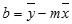
gdzie x i y są średnimi arytmetycznymi, tj. x = ŚREDNIA(znane_x) i y = ŚREDNIA(znane_y).
-
Funkcje reglinii i krzywej REGLINP i REGLINP mogą obliczyć najlepszą linię prostą lub krzywą wykładniczą pasującą do danych. Musisz jednak zdecydować, który z tych dwóch wyników najlepiej pasuje do Twoich danych. Można obliczyć wartość REGLINW(known_y;known_x) dla linii prostej lub funkcji REGEXPW(known_y;known_x) dla krzywej wykładniczej. Te funkcje bez argumentu new_x zwracają tablicę wartości y przewidywanych wzdłuż tej linii lub krzywej w rzeczywistych punktach danych. Następnie można porównać przewidywane wartości z wartościami rzeczywistymi. Warto je utworzyć na obu wykresach w celu porównania wizualnego.
-
W przypadku analizy metodą regresji program Excel oblicza dla każdego punktu kwadrat różnicy pomiędzy wartością y szacowaną dla tego punktu a jego rzeczywistą wartością y. Suma kwadratów różnic nazywana jest resztkową sumą kwadratów (ssresid). Następnie program Excel oblicza całkowitą sumę kwadratów (sstotal). Jeśli argument stała ma wartość PRAWDA lub jest pominięty, łączna suma kwadratów jest sumą kwadratów różnic pomiędzy rzeczywistymi wartościami y a średnią z wartości y. Jeśli argument stała ma wartość FAŁSZ, łączna suma kwadratów jest sumą kwadratów rzeczywistych wartości y (od wartości tych nie jest odejmowana średnia z wartości y). Regresyjna suma kwadratów (ssreg) jest obliczana jako różnica łącznej sumy kwadratów i resztkowej sumy kwadratów. Mniejsza jest resztkowa suma kwadratów w porównaniu z całkowitą sumą kwadratów, tym większa jest wartość współczynnika oznaczania r2, co jest wskaźnikiem tego, jak dobrze równanie wynikające z analizy regresji wyjaśnia relację między zmiennymi. Wartość r2 jest równa wartości ssreg/sstotal.
-
W niektórych przypadkach co najmniej jedna kolumna X (załóżmy, że kolumny Y i X znajdują się w kolumnach) może nie mieć żadnej dodatkowej wartości predykcyjnej w obecności pozostałych kolumn X. Innymi słowy, wyeliminowanie jednej lub większej liczby kolumn X może prowadzić do równie dokładnych przewidywanych wartości Y. W takim przypadku nadmiarowe kolumny X powinny zostać pominięte w modelu regresji. Zjawisko to nazywa się "współliniowością", ponieważ każdą nadmiarową kolumnę X można wyrazić jako sumę wielokrotności nie nadmiarowych kolumn X. Funkcja REGLINP sprawdza współliniowość i usuwa zbędne kolumny X z modelu regresji, gdy je identyfikuje. Usunięte kolumny X można rozpoznać w wynikach funkcji REGLINP jako mające 0 współczynników oprócz wartości 0 se. Jeśli co najmniej jedna kolumna zostanie usunięta jako nadmiarowa, problem dotyczy df, ponieważ wartość df zależy od liczby kolumn X faktycznie używanych do przewidywania. Aby uzyskać szczegółowe informacje na temat obliczania wartości df, zobacz Przykład 4. Jeśli wartość df zostanie zmieniona, ponieważ usuwane są nadmiarowe kolumny X, mają one również wpływ na wartości sey i F. Współliniowość powinna być stosunkowo rzadka w praktyce. Jednak bardziej prawdopodobne jest, że niektóre kolumny X zawierają tylko wartości 0 i 1 jako wskaźniki tego, czy temat eksperymentu jest członkiem określonej grupy, czy nie. Jeśli argument stała = PRAWDA lub zostanie pominięty, funkcja REGLINP skutecznie wstawia dodatkową kolumnę X zawierającą wszystkie 1 wartości w celu modelowania przecięcia. Jeśli masz kolumnę z 1 dla każdego tematu, jeśli mężczyzna, lub 0, jeśli nie, i masz również kolumnę z 1 dla każdego tematu, jeśli kobieta, lub 0, jeśli nie, ta ostatnia kolumna jest zbędna, ponieważ wpisy w niej można uzyskać odejmowania wpisu w kolumnie "wskaźnik męski" od wpisu w dodatkowej kolumnie wszystkich 1 wartości dodanych przez funkcję REGLINP .
-
Gdy z modelu nie są usuwane żadne kolumny X z powodu zależności liniowej, wartość df jest obliczana w następujący sposób: jeśli istnieje k kolumn znane_x i argument stała ma wartość PRAWDA lub jest pominięty, to df = n – k – 1. Jeśli argument stała ma wartość FAŁSZ, to df = n – k. W obydwu wypadkach każde usunięcie liniowo zależnej kolumny X powoduje zwiększenie wartości df o 1.
-
Gdy jako argument jest wprowadzana stała tablicowa, taka jak znane_x, wartości w tym samym wierszu należy rozdzielać średnikami, a wartości w tej samej kolumnie ukośnikami odwrotnymi (\). Znaki separatorów mogą być inne, w zależności od ustawień regionalnych.
-
Należy zauważyć, że wartości y przewidziane przez równanie regresyjne mogą być nieprawidłowe, jeśli znajdują się poza zakresem wartości y użytym dla określenia równania.
-
Algorytm używany w funkcji REGLINP jest inny niż algorytm używany w funkcjach NACHYLENIE i ODCIĘTA. Różnica między tymi algorytmami może prowadzić do innych wyników, gdy dane są nieokreślone i współliniowe. Jeśli na przykład punkty danych argumentu znane_y mają wartość 0, a punkty danych argumentu znane_x mają wartość 1:
-
Funkcja REGLINP zwraca wartość 0. Algorytm funkcji REGLINP ma zwracać rozsądne wyniki dla danych współliniowych, a w tym przypadku można znaleźć co najmniej jedną odpowiedź.
-
FUNKCJE NACHYLENIE i ODCIĘTA zwracają wartość #DIV/0! . Algorytm funkcji NACHYLENIE i ODCIĘTA jest przeznaczony do wyszukiwania tylko jednej odpowiedzi, a w tym przypadku może być więcej niż jedna odpowiedź.
-
-
Oprócz obliczania statystki dla innych typów regresji za pomocą funkcji REGEXPP, przy użyciu funkcji REGLINP można obliczać zakres innych typów regresji, wprowadzając funkcje zmiennych x i y jako serie x i y dla funkcji REGLINP. Na przykład następująca formuła:
=REGLINP(wartości_y; wartości_x^NR.KOLUMNY($A:$C))
działa, gdy pojedyncza kolumna wartości y i pojedyncza kolumna wartości x zostaną użyte do obliczenia sześciennego przybliżenia formuły (wielomianu rzędu 3):
y = m1*x + m2*x^2 + m3*x^3 + b
Można dostosować tę formułę do obliczania innych typów regresji, ale w niektórych przypadkach wymaga to dopasowania wartości wyjściowych i innych statystyk.
-
Wartość testu F zwracana przez funkcję REGLINP różni się od wartości testu F zwracanej przez funkcję TEST.F. Funkcja REGLINP zwraca statystykę F, natomiast funkcja TEST.F zwraca prawdopodobieństwo.
Przykłady
Przykład 1. Nachylenie i punkt przecięcia osi y
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Znane y |
Znane x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Wynik (nachylenie) |
Wynik (przecięcie z osią y) |
|
2 |
1 |
|
Formuła (formuła tablicowa w komórkach A7:B7) |
|
|
=REGLINP(A2:A5;B2:B5;;FAŁSZ) |
Przykład 2. Prosta regresja liniowa
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Miesiąc |
Sprzedaż |
|---|---|
|
1 |
3100 zł |
|
2 |
4500 zł |
|
3 |
4400 zł |
|
4 |
5400 zł |
|
5 |
7500 zł |
|
6 |
8100 zł |
|
Formuła |
Wynik |
|
=SUMA(REGLINP(B1:B6;A1:A6)*{9;1}) |
11 000 zł |
|
Oblicza szacowaną sprzedaż w dziewiątym miesiącu na podstawie sprzedaży od pierwszego do szóstego miesiąca. |
Przykład 3. Wielokrotna regresja liniowa
Skopiuj przykładowe dane z poniższej tabeli i wklej je w komórce A1 nowego arkusza programu Excel. Aby formuły wyświetlały wyniki, zaznacz je, naciśnij klawisz F2, a następnie naciśnij klawisz Enter. Jeśli to konieczne, możesz dostosować szerokości kolumn, aby wyświetlić pełne dane.
|
Powierzchnia budynku (x1) |
Liczba lokali biurowych (x2) |
Liczba wejść (x3) |
Wiek budynku (x4) |
Szacowana wartość budynku (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142 000 zł |
|
2333 |
2 |
2 |
12 |
144 000 zł |
|
2356 |
3 |
1,5 |
33 |
151 000 zł |
|
2379 |
3 |
2 |
43 |
150 000 zł |
|
2402 |
2 |
3 |
53 |
139 000 zł |
|
2425 |
4 |
2 |
23 |
169 000 zł |
|
2448 |
2 |
1,5 |
99 |
126 000 zł |
|
2471 |
2 |
2 |
34 |
142 900 zł |
|
2494 |
3 |
3 |
23 |
163 000 zł |
|
2517 |
4 |
4 |
55 |
169 000 zł |
|
2540 |
2 |
3 |
22 |
149 000 zł |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Formuła (dynamiczna formuła tablicowa wprowadzona w komórce A19) |
||||
|
=REGLINP(E2:E12;A2:D12;PRAWDA;PRAWDA) |
Przykład 4. Używanie statystyk F i r2
W poprzednim przykładzie współczynnik oznaczania (r2) wynosi 0,99675 (patrz komórka A17 w wyniku funkcji REGLINP), co oznaczałoby silną relację między zmiennymi niezależnymi a ceną sprzedaży. Można zastosować statystykę F do określenia, czy wyniki te, przy tak wysokiej wartości r2, wystąpiły przypadkowo.
Przyjmijmy na chwilę, że w rzeczywistości nie ma żadnej relacji pomiędzy zmiennymi, ale została przyjęta rzadka próbka 11 biurowców, która powoduje, że analiza statystyczna wykazuje ścisłą relację. Dla prawdopodobieństwa błędnego wnioskowania o istnieniu zależności stosowane jest określenie „Alfa”.
Wartości F i df w wynikach z funkcji REGLINP mogą być używane do oceny prawdopodobieństwa wystąpienia wyższej wartości F przez przypadek. F można porównać z wartościami krytycznymi w opublikowanych tabelach rozkładu F lub funkcji ROZKŁAD.F w programie Excel, aby obliczyć prawdopodobieństwo wystąpienia większej wartości F przez przypadek. Odpowiedni rozkład F ma wartość v1 i v2 stopni swobody. Jeśli n jest liczbą punktów danych i stała = PRAWDA lub pominięta, to v1 = n – df – 1 i v2 = df. (Jeśli stała = FAŁSZ, to v1 = n – df i v2 = df). Funkcja ROZKŁAD.F — ze składnią ROZKŁAD.F(F;v1;v2) — zwróci prawdopodobieństwo wystąpienia wyższej wartości F przez przypadek. W tym przykładzie df = 6 (komórka B18) i F = 459,753674 (komórka A18).
Zakładając, że Alfa = 0,05, v1 = 11 – 6 – 1 = 4 i v2 = 6, wartość krytyczna F wynosi 4,53. Ponieważ F = 459,753674 jest dużo większe od 4,53, prawdopodobieństwo przyjęcia przez F tak dużej wartości jest bardzo małe. (Na poziomie Alfa = 0,05 hipoteza o braku zależności między wartościami w tablicy Znane_y i tablicy Znane_x powinna zostać odrzucona, gdy F przekracza wartość krytyczną 4,53). Z pomocą funkcji ROZKŁAD.F programu Excel można obliczyć prawdopodobieństwo, że wartość F przyjmie większą wartość. Na przykład ROZKŁAD.F(459,753674; 4; 6) = 1,37E-7, czyli jest to prawdopodobieństwo bardzo małe. Odszukując krytyczny poziom wartości F w tablicach lub używając funkcji ROZKŁAD.F można wysnuć wniosek, że równanie regresji jest przydatne do oszacowania przewidywanej wartości badanych biurowców w tym obszarze. Należy jednak pamiętać o przyjęciu prawidłowych wartości v1 i v2 (obliczanych metodą podaną w poprzednim akapicie).
Przykład 5. Obliczanie statystyki t
Inny hipotetyczny test będzie określać, czy można korzystać z każdego współczynnika nachylenia podczas oceny szacunkowej wartości biurowca w przykładzie 3. Na przykład, aby sprawdzić znaczenie statystyczne współczynnika wieku budynku, należy podzielić -234,24 (współczynnik nachylenia odpowiadający wiekowi) przez 13,268 (szacunkowy standardowy błąd współczynników wieku w komórce A15). Obserwowaną wartość t podano poniżej:
t = m4 ÷ se4 = -234,24 ÷ 13,268 = -17,7
Jeśli wartość bezwzględna jest wystarczająco duża, można przyjąć, że obliczony współczynnik nachylenia jest użyteczny w oszacowaniu przewidywanej wartości biurowca omawianego w przykładzie 3. W poniższej tabeli pokazano wartości bezwzględne dla 4 obserwacji.
Jeśli skonsultujesz się z tabelą w podręczniku statystycznym, przekonasz się, że wartość krytyczna t, dwustronna, z 6 stopniami swobody, a Alfa = 0,05 to 2,447. Tę wartość krytyczną można również znaleźć przy użyciu funkcji ROZKŁAD.T.ODW w programie Excel. ROZKŁAD.T.ODW(0,05;6) = 2,447. Ponieważ wartość bezwzględna t (17,7) jest większa niż 2,447, wiek jest istotną zmienną przy szacowaniu szacunkowej wartości biurowca. Każdą z pozostałych zmiennych niezależnych można przetestować pod kątem istotności statystycznej w podobny sposób. Poniżej przedstawiono obserwowane wartości t dla każdej zmiennej niezależnej.
|
Zmienna |
Wartość obserwowana t |
|---|---|
|
Powierzchnia budynku |
5,1 |
|
Liczba lokali biurowych |
31,3 |
|
Liczba wejść |
4,8 |
|
Wiek budynku |
17,7 |
Wartość bezwzględna wszystkich wartości jest większa niż 2,447, a zatem wszystkie zmienne użyte w równaniu regresji są użyteczne w prognozowaniu szacunkowej wartości biurowców na tym terenie.










