Uwaga: Staramy się udostępniać najnowszą zawartość Pomocy w Twoim języku tak szybko, jak to możliwe. Ta strona została przetłumaczona automatycznie i może zawierać błędy gramatyczne lub nieścisłości. Chcemy, aby ta zawartość była dla Ciebie przydatna. Prosimy o powiadomienie nas, czy te informacje były pomocne, u dołu tej strony. Oto angielskojęzyczny artykuł do wglądu.
Zwraca wartość bieżącą inwestycji. Wartość bieżąca to kwota całkowita, określająca bieżącą wartość serii przyszłych płatności. Na przykład gdy pożyczasz pieniądze, kwota pożyczki jest wartością bieżącą dla pożyczkodawcy.
Składnia
PV(stopa;liczba_rat;rata;wp;typ)
Stopa to stopa procentowa dla okresu. Na przykład osoba otrzymująca pożyczkę na samochód, oprocentowaną na 10 procent rocznie, spłacająca tę pożyczkę w miesięcznych ratach, będzie płacić miesięczne oprocentowanie w wysokości 10%/12, czyli 0,83%. Dlatego jako oprocentowanie należy wprowadzić do formuły wartość 10%/12 albo 0,83%, albo 0,0083.
Liczba_rat to całkowita liczba okresów płatności w okresie spłaty. Na przykład osoba otrzymująca czteroletnią pożyczkę na samochód, spłacająca tę pożyczkę w miesięcznych ratach, będzie ją spłacać w ciągu 4*12 (czyli 48) okresów. Dlatego jako argument liczba_rat należy wprowadzić do formuły liczbę 48.
Rata to płatność dokonywana w każdym okresie, nie zmieniana przez cały okres pożyczki. Rata obejmuje zazwyczaj kapitał i odsetki z wyłączeniem innych opłat i podatków. Na przykład miesięczna spłata czteroletniej pożyczki na samochód w wysokości 10 000 zł, oprocentowanej na 12 %, wynosi 263,33 zł. Jako argument rata należy wprowadzić do formuły wartość -263,33. Jeśli argument rata zostanie pominięty, musi zostać dołączony argument wp.
Wp to przyszła wartość, czyli poziom finansowy, do którego zmierza się po dokonaniu ostatniej płatności. Jeśli argument jest pominięty, to jako jego wartość przyjmuje się 0 (przyszła wartość pożyczki na przykład wynosi 0). Na przykład, jeśli chce się zaoszczędzić 50 000 zł w ciągu 18 lat na określony cel, to 50 000 zł jest wartością przyszłą. Zakładając pewną stopę procentową można obliczyć, ile pieniędzy trzeba odkładać co miesiąc. Jeśli argument wp jest pominięty, musi zostać dołączony argument rata.
Typ to liczba 0 lub 1, która wskazuje termin płatności.
|
Typ |
Termin płatności |
|
0 lub jest pominięty |
koniec okresu |
|
2,54 |
początek okresu |
Spostrzeżenia
-
Upewnij się, że definiując stawkę i parametr Lokr, stosujesz wszędzie te same jednostki. Jeżeli dokonujesz comiesięcznych płatności czteroletniej pożyczki oprocentowanej w skali 12 procent rocznie, użyj formatu 12%/12 w przypadku stawki i formatu 4*12 w przypadku parametru Lokr. Jeżeli spłacasz tę samą pożyczkę, dokonując płatności raz w roku, użyj formatu 12% w przypadku stawki i formatu 4 w przypadku parametru Lokr.
-
Następujące funkcje odnoszą się do płatności ratalnych: FV, IPMT, PMT, PPMT, PV i RATE. Płatność ratalna to seria stałych płatności gotówkowych dokonywanych w ciągłym okresie. Na przykład kredyt samochodowy lub pożyczka hipoteczna są płatnościami ratalnymi. Aby uzyskać więcej informacji, zapoznaj się z opisami poszczególnych funkcji płatności ratalnych.
-
W funkcjach płatności annuitetowych wypłacana gotówka, np. jako depozyt przekazywany na konto oszczędnościoweto savings, jest wyrażana liczbą ujemną; otrzymana gotówka, np. czek na wypłatę dywidendy, jest wyrażona liczbą dodatnią. Na przykład depozyt bankowy w wysokości 1000 PLN jest wyrażony argumentem -1000 w przypadku osoby deponującej i argumentem 1000 w przypadku banku.
-
Jeden argument finansowy jest rozpatrywany w zależności od innych. Jeśli stopa jest różna od zera, to:
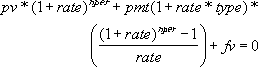
Jeśli stopa jest równa zero:
(rata* liczba_rat) + wa + wp = 0
Przykład
W poniższym przykładzie:
-
Rata to pieniądze wypłacane jako płatności annuitetowe z polisy ubezpieczeniowej na koniec każdego miesiąca.
-
Stopa to procent od wypłaconych pieniędzy.
-
Liczba_rat określająca liczbę lat, w których będą wypłacane pieniądze.
Stopa odsetek jest dzielona przez 12 w celu uzyskania stawki miesięcznej. Lata, w których są wypłacane pieniądze, są mnożone przez 12 w celu uzyskania liczby płatności.
|
Rata |
Stopa |
Liczba_okresów |
Formuła: |
Opis (wynik) |
|
500 |
8% |
20 |
=PV([Stopa]/12; 12*[Liczba_okresów]; [Rata]; ; 0) |
Wartość bieżąca płatności annuitetowej z określonymi argumentami (-59 777,15). |
Wynik jest ujemny, ponieważ określa pieniądze, które zostaną wypłacone (przepływ pieniędzy na zewnątrz). Jeżeli musisz dokonać płatności annuitetowej (60 000), musisz określić, że nie będzie to dobra inwestycja, ponieważ wartość bieżąca płatności annuitetowej (59 777,15) jest mniejsza niż kwota, którą musisz zapłacić.










