Als u complexe statistische of technische analyses wilt ontwikkelen, kunt u stappen en tijd besparen met analysis toolPak. U geeft de gegevens en parameters voor elke analyse op en het hulpprogramma gebruikt de juiste statistische of technische macrofuncties om de resultaten in een uitvoertabel te berekenen en weer te geven. Sommige hulpprogramma's genereren grafieken naast uitvoertabellen.
De functies voor gegevensanalyse kunnen slechts in één werkblad tegelijk worden gebruikt. Als u gegevens in gegroepeerde werkbladen analyseert, worden de resultaten in het eerste werkblad weergegeven en worden in de overige werkbladen lege, opgemaakte tabellen weergegeven. Als u de gegevensanalyse ook in de overige werkbladen wilt toepassen, moet u het analysehulpmiddel op elk werkblad opnieuw toepassen.
Analysis ToolPak bevat de hulpmiddelen die in de volgende secties worden beschreven. Deze hulpmiddelen opent u door op Gegevensanalyse te klikken in de groep Analyse van het tabblad Gegevens. Als de opdracht Gegevensanalyse niet beschikbaar is, moet u de invoegtoepassing Analysis ToolPak laden.
-
Klik op het tabblad Bestand op Opties en klik op de categorie Invoegtoepassingen.
-
Selecteer in het vak Beheren de optie Excel-invoegtoepassingen en klik op Start.
Als u Excel voor Mac gebruikt, gaat u in het bestandsmenu naar Extra > Excel-invoegtoepassingen.
-
Selecteer in het vak Invoegtoepassingen het selectievakje Analysis ToolPak en klik vervolgens op OK .
-
Als Analysis ToolPak niet voorkomt in het vak Beschikbare invoegtoepassingen, klikt u op Bladeren om naar de invoegtoepassing te zoeken.
-
Als u het bericht krijgt dat Analysis ToolPak niet is geïnstalleerd op uw computer, klikt u op Ja om de invoegtoepassing te installeren.
-
Opmerking: Als u in Analysis ToolPak gebruik wilt maken van de functies van Visual Basic for Applications (VBA), laadt u de invoegtoepassing Analysis ToolPak - VBA op dezelfde manier als u Analysis ToolPak laadt. Schakel in het vak Beschikbare invoegtoepassingen het selectievakje Analysis ToolPak - VBA in.
De hulpmiddelen voor variantieanalyse bieden verschillende typen variantieanalyses. Welk hulpmiddel u het best kunt gebruiken, hangt af van het aantal factoren en het aantal steekproeven dat u neemt van de te toetsen populaties.
Unifactoriële variantieanalyse
Met dit hulpprogramma wordt een eenvoudige analyse van variantie uitgevoerd op gegevens voor twee of meer voorbeelden. De analyse biedt een test van de hypothese dat elke steekproef wordt getrokken uit dezelfde onderliggende kansverdeling ten opzichte van de alternatieve hypothese dat onderliggende kansverdelingen niet voor alle steekproeven hetzelfde zijn. Als er slechts twee voorbeelden zijn, kunt u de werkbladfunctie T gebruiken.TEST. Met meer dan twee steekproeven is er geen handige generalisatie van T.TEST en het Single Factor Anova-model kunnen in plaats daarvan worden aangeroepen.
Multifactoriële variantieanalyse met herhaling
Dit analysehulpmiddel is geschikt als gegevens kunnen worden geclassificeerd volgens twee verschillende dimensies. Bijvoorbeeld: in een experiment waarbij de hoogte van planten wordt gemeten, kunt u de planten verschillende merken kunstmest geven (merk A, B en C) en bij verschillende temperaturen kweken (hoog en laag). Voor elk van de zes mogelijke combinaties van kunstmest en temperatuur hebben we een gelijk aantal waarnemingen van de planthoogte. Met dit hulpmiddel kunnen we toetsen:
-
Of hoogten van planten voor de verschillende merken kunstmest uit dezelfde onderliggende populatie zijn getrokken. De temperaturen worden voor deze analyse genegeerd.
-
Of hoogten van planten voor de verschillende temperatuurniveaus uit dezelfde onderliggende populatie zijn getrokken. De kunstmestmerken worden voor deze analyse genegeerd.
Volgens de nulhypothese worden de zes steekproeven die alle combinaties van kunstmest en temperatuur vertegenwoordigen, uit dezelfde populatie getrokken, ongeacht of er nu een verklaring is gevonden voor de effecten van verschillen tussen kunstmestmerken die zijn aangetroffen bij stap 1 en verschillen in temperaturen die zijn aangetroffen bij stap 2. Volgens de alternatieve hypothese zijn er effecten die zijn toe te schrijven aan specifieke combinaties van kunstmest en temperatuur, buiten verschillen op basis van alleen kunstmest of van alleen temperatuur.
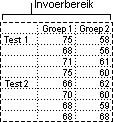
Multifactoriële variantieanalyse zonder herhaling
Dit analysehulpmiddel is geschikt als gegevens een waarde hebben in twee verschillende dimensies, net als bij de multifactoriële variantieanalyse met herhaling. Bij dit hulpmiddel nemen we echter aan dat er voor elk paar (bijvoorbeeld elke combinatie van kunstmest en temperatuur in het bovenstaande voorbeeld) maar één waarneming is.
De werkbladfuncties CORRELATIE en PEARSON berekenen beide de correlatiecoëfficient tussen twee meetvariabelen wanneer metingen op elke variabele worden waargenomen voor elk van n proefpersonen. (Als een waarneming ontbreekt voor een proefpersoon, wordt deze proefpersoon in de analyse genegeerd.) Het analysehulpmiddel Correlatie is met name geschikt wanneer er meer dan twee meetvariabelen voor elk van n proefpersonen zijn. In de uitvoertabel, een correlatiematrix, wordt de waarde van CORRELATIE (of PEARSON) weergegeven voor elk mogelijk paar meetvariabelen.
Net als de covariantie geeft de correlatiecoëfficiënt aan in welke mate twee meetvariabelen 'gezamenlijk variëren'. Anders dan bij de covariantie is de waarde van de correlatiecoëfficiënt onafhankelijk van de eenheden waarin de twee meetvariabelen worden uitgedrukt. Als de twee meetvariabelen bijvoorbeeld gewicht en hoogte zijn, blijft de waarde van de correlatiecoëfficient ongewijzigd als het gewicht wordt geconverteerd van ponden naar kilo's. In elke correlatiecoëfficiënt wordt de covariantie omgerekend naar een waarde van minimaal -1 en maximaal +1.
Met het hulpmiddel Correlatie kunt u elk paar meetvariabelen onderzoeken om vast te stellen in welke mate de twee meetvariabelen met elkaar samenhangen. Bij een positieve correlatie gaan grote waarden in de ene variabele samen met grote waarden in de andere variabele. Als kleine waarden in de ene variabele samengaan met grote waarden in de andere variabele, is er sprake van een negatieve correlatie. Het is ook mogelijk dat de waarden van beide variabelen geen of weinig samenhang vertonen. In dat geval nadert de correlatie de waarde 0 (nul).
De hulpprogramma's Correlatie en Covariantie kunnen beide in dezelfde instelling worden gebruikt, wanneer u N verschillende meetvariabelen hebt waargenomen op een set individuen. De hulpprogramma's Correlatie en Covariantie geven elk een uitvoertabel, een matrix, waarin respectievelijk de correlatiecoëfficiënt of covariantie tussen elk paar meetvariabelen wordt weergegeven. Het verschil is dat correlatiecoëfficiënten worden geschaald om tussen -1 en +1 te liggen. Overeenkomende covariantieën worden niet geschaald. Zowel de correlatiecoëfficiënt als de covariantie zijn maatstaven voor de mate waarin twee variabelen 'samen variëren'.
Het hulpprogramma Covariantie berekent de waarde van de werkbladfunctie COVARIANTIE. P voor elk paar meetvariabelen. (Direct gebruik van COVARIANTIE. P in plaats van het hulpprogramma Covariantie is een redelijk alternatief wanneer er slechts twee meetvariabelen zijn, namelijk N=2.) De vermelding op de diagonaal van de uitvoertabel van het hulpmiddel Covariantie in rij i, kolom i is de covariantie van de meetvariabele i-th met zichzelf. Dit is alleen de variantie van de populatie voor die variabele, zoals berekend door de werkbladfunctie VAR.P.
Met het hulpmiddel Covariantie kunt u elk paar meetvariabelen onderzoeken om vast te stellen in welke mate de twee meetvariabelen met elkaar samenhangen. Bij een positieve covariantie gaan grote waarden in de ene variabele samen met grote waarden in de andere variabele. Als kleine waarden in de ene variabele samengaan met grote waarden in de andere variabele, is er sprake van een negatieve covariantie. Het is ook mogelijk dat de waarden van beide variabelen geen of weinig samenhang vertonen. In dat geval nadert de covariantie de waarde nul.
Met het analysehulpmiddel Beschrijvende statistiek wordt een univariaat statistisch rapport gegenereerd voor gegevens in het invoerbereik. Het rapport geeft informatie over de centrale trend en de variabiliteit van de gegevens.
Het analyseprogramma voor exponentieel vloeiend maken voorspelt een waarde die is gebaseerd op de prognose voor de voorgaande periode, aangepast voor de fout in die eerdere prognose. Het hulpprogramma maakt gebruik van de afvlakkingsconstante a, waarvan de grootte bepaalt hoe sterk de prognoses reageren op fouten in de eerdere prognose.
Opmerking: Waarden tussen 0,2 en 0,3 zijn redelijke dempingsconstanten. Deze waarden geven aan dat de huidige voorspelling met 20 tot 30 procent moet worden bijgesteld vanwege fouten in de voorgaande voorspelling. Als u een hogere waarde opgeeft, worden de resultaten sneller berekend, maar neemt de kans op foutieve voorspellingen toe. Lagere waarden kunnen leiden tot grote vertragingen bij het berekenen van de waarden.
Met het analysehulpmiddel F-toets voor twee steekproeven op varianties worden de populatievarianties van twee steekproeven getoetst.
U kunt het hulpmiddel F-toets bijvoorbeeld gebruiken bij steekproeven van de tijden die door twee teams zijn behaald bij een zwemwedstrijd. Het hulpmiddel geeft de uitkomst van een toets van de nulhypothese dat deze twee steekproeven behoren tot verdelingen met gelijke varianties ten opzichte van de alternatieve hypothese dat de varianties niet gelijk zijn in de onderliggende verdelingen.
Het hulpprogramma berekent de waarde f van een F-statistiek (of F-verhouding). Een waarde van f dicht bij 1 biedt bewijs dat de onderliggende populatievariantie gelijk is. Als in de uitvoertabel f < 1 "P(F <= f) one-tail" geeft de kans op het observeren van een waarde van de F-statistiek kleiner dan f wanneer de populatievariantie gelijk is, en "F Critical one-tail" geeft de kritieke waarde kleiner dan 1 voor het gekozen significantieniveau, Alfa. Als f > 1, geeft "P(F <= f) one-tail" de kans op het observeren van een waarde van de F-statistiek groter dan f wanneer de populatievariantie gelijk is, en "F Critical one-tail" geeft de kritieke waarde groter dan 1 voor Alfa.
Het hulpprogramma Fourier-analyse lost problemen in lineaire systemen op en analyseert periodieke gegevens met behulp van de FFT-methode (Fast Fourier Transform) om gegevens te transformeren. Dit hulpprogramma ondersteunt ook inverse transformaties, waarbij de inverse van getransformeerde gegevens de oorspronkelijke gegevens retourneert.
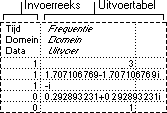
Met het analysehulpmiddel Histogram worden afzonderlijke en cumulatieve frequenties berekend voor een cellenbereik met gegevens en grenswaarden. U kunt met dit hulpmiddel bepalen hoe vaak een bepaalde waarde in een gegevensverzameling voorkomt.
Als u bijvoorbeeld wilt weten hoe in een klas met twintig leerlingen de proefwerkcijfers in bepaalde categorieën zijn verdeeld, kunt u dat met dit hulpmiddel bepalen. Een histogram laat zien welke cijfers de begrenzing van de categorieën vormen en geeft het aantal cijfers tussen de benedengrens en de huidige grens weer. Het meest behaalde cijfer is dan de modus van het gegevensbereik.
Tip: In Excel 2016 kunt u nu een histogram of Paretografiek maken.
Het analysehulpmiddel Zwevend gemiddelde projecteert waarden in de voorspellingsperiode, op basis van de gemiddelde waarde van de variabele over een bepaald aantal voorafgaande perioden. Een zwevend gemiddelde geeft informatie over trends die moeilijk te herkennen zijn in een eenvoudig gemiddelde van alle historische gegevens. U kunt dit hulpmiddel gebruiken voor verkoopprognoses, voorraadprognoses en andere trends. Elke voorspellingswaarde is gebaseerd op de volgende formule:
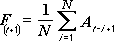
waarbij:
-
N het aantal voorgaande perioden is dat in het zwevend gemiddelde wordt opgenomen.
-
A j de actuele waarde is op het moment j
-
F j de voorspellingswaarde is op het moment j
Met het analysehulpmiddel Aselecte getallen wordt een bereik gevuld met onafhankelijke willekeurige getallen die uit één van een aantal afzonderlijke verdelingen worden getrokken. U kunt dit hulpmiddel gebruiken om aan onderdelen van een populatie een kansverdeling toe te kennen. U kunt bijvoorbeeld een normale verdeling toekennen aan een populatie bestaande uit de lichaamslengte van personen, of een Bernoulli-verdeling van twee mogelijke waarden aan de populatie bestaande uit de uitkomsten van een 'kruis-of-munt'-proef.
Het hulpmiddel Rangschikking en percentielanalyse produceert een tabel die de rangschikking en het percentage van elke waarde in een gegevensset bevat. U kunt de relatieve positie van waarden in een gegevensset analyseren. Dit hulpprogramma maakt gebruik van de werkbladfuncties RANK. EQ enPERCENTRANK. INC. Als u rekening wilt houden met gekoppelde waarden, gebruikt u de RANG. EQ - functie, die gekoppelde waarden als dezelfde rangschikking behandelt of de RANG gebruikt.De functie AVG , die de gemiddelde rangschikking voor de gekoppelde waarden retourneert.
Het hulpprogramma Regressieanalyse voert lineaire regressieanalyse uit met behulp van de methode 'kleinste kwadraten' om een lijn door een reeks waarnemingen te passen. U kunt analyseren hoe één afhankelijke variabele wordt beïnvloed door de waarden van een of meer onafhankelijke variabelen. U kunt bijvoorbeeld analyseren hoe de prestaties van een atleet worden beïnvloed door factoren zoals leeftijd, lengte en gewicht. U kunt aandelen in de prestatiemeting toewijzen aan elk van deze drie factoren, op basis van een set prestatiegegevens, en vervolgens de resultaten gebruiken om de prestaties van een nieuwe, niet-geteste atleet te voorspellen.
Het hulpprogramma Regressie maakt gebruik van de werkbladfunctie LIJNENT.
Met het analysehulpmiddel Steekproef wordt een steekproef uit een populatie genomen, waarbij het invoerbereik als een populatie wordt beschouwd. Als de populatie te groot is om te verwerken of in een grafiek weer te geven, kunt u gebruikmaken van een representatieve steekproef. Bovendien kunt u, als het invoerbereik periodieke gegevens bevat, een steekproef nemen die alleen waarden bevat uit een bepaald deel van de cyclus. Als het invoerbereik bijvoorbeeld kwartaalcijfers bevat, worden bij een steekproef met een periodiek van 4 de waarden uit hetzelfde kwartaal in de uitvoertabel geplaatst.
De analysehulpmiddelen voor de t-toets met twee gepaarde steekproeven testen of de populatiegemiddelden van elke steekproef gelijk zijn. De drie hulpmiddelen gaan uit van verschillende veronderstellingen: dat de populatievarianties gelijk zijn, dat de populatievarianties niet gelijk zijn, en dat de twee steekproeven voor en na behandeling waarnemingen weergeven over dezelfde onderdelen.
Voor alle drie onderstaande hulpmiddelen wordt een toetsingsgrootheid T berekend en weergegeven als 't Stat' in de uitvoertabellen. Afhankelijk van de gegevens kan deze waarde T negatief of niet-negatief zijn. Uitgaande van gelijke onderliggende populatiegemiddelden, als t < 0, geeft 'P(T <= t) eenzijdig' de kans dat een waarde van de toetsingsgrootheid T wordt waargenomen die negatiever is dan t. Als t >=0, geeft 'P(T <= t) eenzijdig' de kans dat een waarde van de toetsingsgrootheid T wordt waargenomen die positiever is dan t. 'Eenzijdige kritische t-waarde' geeft de grenswaarde waarbij de kans een waarde van de toetsingsgrootheid T groter dan of gelijk aan de 'eenzijdige kritische t-waarde' waar te nemen, gelijk is aan alfa.
'P(T <= t) tweezijdig' geeft de kans dat een waarde van toetsingsgrootheid T wordt geobserveerd die in absolute waarde groter is dan t. 'Tweezijdige kritische P-waarde' geeft de grenswaarde waarbij de kans van een waargenomen toetsingsgrootheid T in absolute waarde groter dan de 'tweezijdige kritische P-waarde' gelijk is aan alfa.
T-toets: twee gepaarde steekproeven voor gemiddelden
U kunt een gepaarde toets gebruiken wanneer van waarnemingen in de steekproeven natuurlijk gepaard zijn, bijvoorbeeld wanneer een steekproefgroep zowel voor als na een experiment wordt getoetst. Met deze variant van de t-toets voert u een gepaarde t-toets uit op twee steekproeven om vast te stellen of het waarschijnlijk is dat waarnemingen die zijn gedaan vóór een behandeling en waarnemingen die zijn gedaan na een behandeling, behoren tot verdelingen met gelijke populatiegemiddelden. Er wordt bij deze t-toetsvariant niet aangenomen dat de varianties van beide populaties gelijk zijn.
Opmerking: Een van de resultaten van dit hulpmiddel is de gepaarde variantie, een maat voor de spreiding van gegevens om het gemiddelde. De gepaarde variantie wordt afgeleid uit de volgende formule:
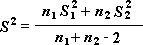
T-toets: twee gepaarde steekproeven met gelijke varianties
Met dit analysehulpmiddel voert u een t-toets uit op twee steekproeven. In deze toets wordt ervan uitgegaan dat de twee gegevensverzamelingen behoren tot verdelingen met gelijke varianties. De toets wordt daarom ook wel een homoscedastische t-toets genoemd. Met deze t-toets kunt u vaststellen of het waarschijnlijk is dat de twee steekproeven behoren tot verdelingen met gelijke populatiegemiddelden.
T-toets: twee gepaarde steekproeven met ongelijke varianties
Met dit analysehulpmiddel voert u een t-toets uit op twee steekproeven. Bij deze variant van de t-toets wordt aangenomen dat de twee gegevensverzamelingen behoren tot verdelingen met ongelijke varianties. Deze toets wordt daarom ook wel een heteroscedastische t-toets genoemd. Net als bij de eerder besproken t-toets met twee gepaarde steekproeven met gelijke varianties kunt met deze t-toets vaststellen of het waarschijnlijk is dat de twee steekproeven behoren tot verdelingen met gelijke populatiegemiddelden. Gebruik deze toets als er sprake is van verschillende proefpersonen in de twee steekproeven. Gebruik de hieronder beschreven gepaarde toets als er sprake is van één groep proefpersonen en de twee steekproeven gegevens hebben voor elk onderdeel voor en na een behandeling.
De volgende formule wordt gebruikt om de statistische waarde t vast te stellen:
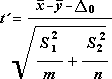
De volgende formule wordt gebruikt om de vrijheidsgraden, df, te berekenen. Omdat het resultaat van de berekening meestal geen geheel getal is, wordt de waarde van df afgerond op het dichtstbijzijnde gehele getal om een kritieke waarde uit de tabel t te verkrijgen. De Excel-werkbladfunctie T.TEST gebruikt de berekende df-waarde zonder afronding, omdat het mogelijk is om een waarde voor T te berekenen.TEST met een niet-integer df. Vanwege deze verschillende benaderingen om de vrijheidsgraden te bepalen, zijn de resultaten van T.TEST en dit t-Test-hulpprogramma verschillen in het geval van ongelijke afwijkingen.
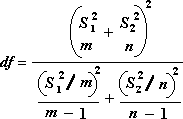
Het analysehulpprogramma z-Test: Two Sample for Means voert een z-test met twee steekproeven uit voor middelen met bekende afwijkingen. Dit hulpprogramma wordt gebruikt om de nulhypothese te testen dat er geen verschil is tussen twee populatiegemiddelden tegen eenzijdige of tweezijdige alternatieve hypothesen. Als afwijkingen niet bekend zijn, gebruikt u de werkbladfunctie Z.In plaats hiervan moet TEST worden gebruikt.
Let op dat u de uitvoer van het hulpmiddel Z-toets goed begrijpt. 'P(Z <= z) eenzijdig' is in feite P(Z >= ABS(z)), de kans op een Z-waarde verder van 0 in dezelfde richting als de waargenomen z-waarde wanneer er geen verschil is tussen de populatiegemiddelden. 'P(Z <= z) tweezijdig' is in feite P(Z >= ABS(z) of Z <= -ABS(z)), de kans op een Z-waarde verder van 0 in een van beide richtingen dan de waargenomen z-waarde wanneer er geen verschil is tussen de populatiegemiddelden. De tweezijdige uitkomst is simpelweg de eenzijdige uitkomst vermenigvuldigd met 2. Het hulpmiddel Z-toets kan ook worden gebruikt wanneer de nulhypothese luidt dat er een specifieke niet-nulwaarde is voor het verschil tussen de twee populatiegemiddelden. U kunt deze toets bijvoorbeeld gebruiken om verschillen tussen de prestaties van twee automodellen vast te stellen.
Meer hulp nodig?
U kunt altijd uw vraag stellen aan een expert in de Excel Tech Community of ondersteuning vragen in de Communities.
Zie ook
Een histogram maken in Excel 2016
Een Pareto-diagram maken in Excel 2016
Analysis ToolPak laden in Excel
ENGINEERING-functies (referentie)
Overzicht van formules in Excel
Niet-werkende formules voorkomen
Fouten in formules zoeken en verbeteren










