This article describes the formula syntax and usage of the LINEST function in Microsoft Excel. Find links to more information about charting and performing a regression analysis in the See Also section.
Description
The LINEST function calculates the statistics for a line by using the "least squares" method to calculate a straight line that best fits your data, and then returns an array that describes the line. You can also combine LINEST with other functions to calculate the statistics for other types of models that are linear in the unknown parameters, including polynomial, logarithmic, exponential, and power series. Because this function returns an array of values, it must be entered as an array formula. Instructions follow the examples in this article.
The equation for the line is:
y = mx + b
–or–
y = m1x1 + m2x2 + ... + b
if there are multiple ranges of x-values, where the dependent y-values are a function of the independent x-values. The m-values are coefficients corresponding to each x-value, and b is a constant value. Note that y, x, and m can be vectors. The array that the LINEST function returns is {mn,mn-1,...,m1,b}. LINEST can also return additional regression statistics.
Syntax
LINEST(known_y's, [known_x's], [const], [stats])
The LINEST function syntax has the following arguments:
Syntax
-
known_y's Required. The set of y-values that you already know in the relationship y = mx + b.
-
If the range of known_y's is in a single column, each column of known_x's is interpreted as a separate variable.
-
If the range of known_y's is contained in a single row, each row of known_x's is interpreted as a separate variable.
-
-
known_x's Optional. A set of x-values that you may already know in the relationship y = mx + b.
-
The range of known_x's can include one or more sets of variables. If only one variable is used, known_y's and known_x's can be ranges of any shape, as long as they have equal dimensions. If more than one variable is used, known_y's must be a vector (that is, a range with a height of one row or a width of one column).
-
If known_x's is omitted, it is assumed to be the array {1,2,3,...} that is the same size as known_y's.
-
-
const Optional. A logical value specifying whether to force the constant b to equal 0.
-
If const is TRUE or omitted, b is calculated normally.
-
If const is FALSE, b is set equal to 0 and the m-values are adjusted to fit y = mx.
-
-
stats Optional. A logical value specifying whether to return additional regression statistics.
-
If stats is TRUE, LINEST returns the additional regression statistics; as a result, the returned array is {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.
-
If stats is FALSE or omitted, LINEST returns only the m-coefficients and the constant b.
The additional regression statistics are as follows.
-
|
Statistic |
Description |
|---|---|
|
se1,se2,...,sen |
The standard error values for the coefficients m1,m2,...,mn. |
|
seb |
The standard error value for the constant b (seb = #N/A when const is FALSE). |
|
r2 |
The coefficient of determination. Compares estimated and actual y-values, and ranges in value from 0 to 1. If it is 1, there is a perfect correlation in the sample — there is no difference between the estimated y-value and the actual y-value. At the other extreme, if the coefficient of determination is 0, the regression equation is not helpful in predicting a y-value. For information about how r2 is calculated, see "Remarks," later in this topic. |
|
sey |
The standard error for the y estimate. |
|
F |
The F statistic, or the F-observed value. Use the F statistic to determine whether the observed relationship between the dependent and independent variables occurs by chance. |
|
df |
The degrees of freedom. Use the degrees of freedom to help you find F-critical values in a statistical table. Compare the values you find in the table to the F statistic returned by LINEST to determine a confidence level for the model. For information about how df is calculated, see "Remarks," later in this topic. Example 4 shows use of F and df. |
|
ssreg |
The regression sum of squares. |
|
ssresid |
The residual sum of squares. For information about how ssreg and ssresid are calculated, see "Remarks," later in this topic. |
The following illustration shows the order in which the additional regression statistics are returned.

Remarks
-
You can describe any straight line with the slope and the y-intercept:
Slope (m):
To find the slope of a line, often written as m, take two points on the line, (x1,y1) and (x2,y2); the slope is equal to (y2 - y1)/(x2 - x1).Y-intercept (b):
The y-intercept of a line, often written as b, is the value of y at the point where the line crosses the y-axis.The equation of a straight line is y = mx + b. Once you know the values of m and b, you can calculate any point on the line by plugging the y- or x-value into that equation. You can also use the TREND function.
-
When you have only one independent x-variable, you can obtain the slope and y-intercept values directly by using the following formulas:
Slope:
=INDEX(LINEST(known_y's,known_x's),1)Y-intercept:
=INDEX(LINEST(known_y's,known_x's),2) -
The accuracy of the line calculated by the LINEST function depends on the degree of scatter in your data. The more linear the data, the more accurate the LINEST model. LINEST uses the method of least squares for determining the best fit for the data. When you have only one independent x-variable, the calculations for m and b are based on the following formulas:
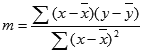
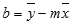
where x and y are sample means; that is, x = AVERAGE(known x's) and y = AVERAGE(known_y's).
-
The line- and curve-fitting functions LINEST and LOGEST can calculate the best straight line or exponential curve that fits your data. However, you have to decide which of the two results best fits your data. You can calculate TREND(known_y's,known_x's) for a straight line, or GROWTH(known_y's, known_x's) for an exponential curve. These functions, without the new_x's argument, return an array of y-values predicted along that line or curve at your actual data points. You can then compare the predicted values with the actual values. You may want to chart them both for a visual comparison.
-
In regression analysis, Excel calculates for each point the squared difference between the y-value estimated for that point and its actual y-value. The sum of these squared differences is called the residual sum of squares, ssresid. Excel then calculates the total sum of squares, sstotal. When the const argument = TRUE or is omitted, the total sum of squares is the sum of the squared differences between the actual y-values and the average of the y-values. When the const argument = FALSE, the total sum of squares is the sum of the squares of the actual y-values (without subtracting the average y-value from each individual y-value). Then regression sum of squares, ssreg, can be found from: ssreg = sstotal - ssresid. The smaller the residual sum of squares is, compared with the total sum of squares, the larger the value of the coefficient of determination, r2, which is an indicator of how well the equation resulting from the regression analysis explains the relationship among the variables. The value of r2 equals ssreg/sstotal.
-
In some cases, one or more of the X columns (assume that Y’s and X’s are in columns) may have no additional predictive value in the presence of the other X columns. In other words, eliminating one or more X columns might lead to predicted Y values that are equally accurate. In that case these redundant X columns should be omitted from the regression model. This phenomenon is called “collinearity” because any redundant X column can be expressed as a sum of multiples of the non-redundant X columns. The LINEST function checks for collinearity and removes any redundant X columns from the regression model when it identifies them. Removed X columns can be recognized in LINEST output as having 0 coefficients in addition to 0 se values. If one or more columns are removed as redundant, df is affected because df depends on the number of X columns actually used for predictive purposes. For details on the computation of df, see Example 4. If df is changed because redundant X columns are removed, values of sey and F are also affected. Collinearity should be relatively rare in practice. However, one case where it is more likely to arise is when some X columns contain only 0 and 1 values as indicators of whether a subject in an experiment is or is not a member of a particular group. If const = TRUE or is omitted, the LINEST function effectively inserts an additional X column of all 1 values to model the intercept. If you have a column with a 1 for each subject if male, or 0 if not, and you also have a column with a 1 for each subject if female, or 0 if not, this latter column is redundant because entries in it can be obtained from subtracting the entry in the “male indicator” column from the entry in the additional column of all 1 values added by the LINEST function.
-
The value of df is calculated as follows, when no X columns are removed from the model due to collinearity: if there are k columns of known_x’s and const = TRUE or is omitted, df = n – k – 1. If const = FALSE, df = n - k. In both cases, each X column that was removed due to collinearity increases the value of df by 1.
-
When entering an array constant (such as known_x's) as an argument, use commas to separate values that are contained in the same row and semicolons to separate rows. Separator characters may be different depending on your regional settings.
-
Note that the y-values predicted by the regression equation may not be valid if they are outside the range of the y-values you used to determine the equation.
-
The underlying algorithm used in the LINEST function is different than the underlying algorithm used in the SLOPE and INTERCEPT functions. The difference between these algorithms can lead to different results when data is undetermined and collinear. For example, if the data points of the known_y's argument are 0 and the data points of the known_x's argument are 1:
-
LINEST returns a value of 0. The algorithm of the LINEST function is designed to return reasonable results for collinear data and, in this case, at least one answer can be found.
-
SLOPE and INTERCEPT return a #DIV/0! error. The algorithm of the SLOPE and INTERCEPT functions is designed to look for only one answer, and in this case there can be more than one answer.
-
-
In addition to using LOGEST to calculate statistics for other regression types, you can use LINEST to calculate a range of other regression types by entering functions of the x and y variables as the x and y series for LINEST. For example, the following formula:
=LINEST(yvalues, xvalues^COLUMN($A:$C))
works when you have a single column of y-values and a single column of x-values to calculate the cubic (polynomial of order 3) approximation of the form:
y = m1*x + m2*x^2 + m3*x^3 + b
You can adjust this formula to calculate other types of regression, but in some cases it requires the adjustment of the output values and other statistics.
-
The F-test value that is returned by the LINEST function differs from the F-test value that is returned by the FTEST function. LINEST returns the F statistic, whereas FTEST returns the probability.
Examples
Example 1 - Slope and Y-Intercept
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Known y |
Known x |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Result (slope) |
Result (y-intercept) |
|
2 |
1 |
|
Formula (array formula in cells A7:B7) |
|
|
=LINEST(A2:A5,B2:B5,,FALSE) |
Example 2 - Simple Linear Regression
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Month |
Sales |
|---|---|
|
1 |
$3,100 |
|
2 |
$4,500 |
|
3 |
$4,400 |
|
4 |
$5,400 |
|
5 |
$7,500 |
|
6 |
$8,100 |
|
Formula |
Result |
|
=SUM(LINEST(B1:B6, A1:A6)*{9,1}) |
$11,000 |
|
Calculates the estimate of the sales in the ninth month, based on sales in months 1 through 6. |
Example 3 - Multiple Linear Regression
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Floor space (x1) |
Offices (x2) |
Entrances (x3) |
Age (x4) |
Assessed value (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
$142,000 |
|
2333 |
2 |
2 |
12 |
$144,000 |
|
2356 |
3 |
1.5 |
33 |
$151,000 |
|
2379 |
3 |
2 |
43 |
$150,000 |
|
2402 |
2 |
3 |
53 |
$139,000 |
|
2425 |
4 |
2 |
23 |
$169,000 |
|
2448 |
2 |
1.5 |
99 |
$126,000 |
|
2471 |
2 |
2 |
34 |
$142,900 |
|
2494 |
3 |
3 |
23 |
$163,000 |
|
2517 |
4 |
4 |
55 |
$169,000 |
|
2540 |
2 |
3 |
22 |
$149,000 |
|
-234.2371645 |
||||
|
13.26801148 |
||||
|
0.996747993 |
||||
|
459.7536742 |
||||
|
1732393319 |
||||
|
Formula (dynamic array formula entered in A19) |
||||
|
=LINEST(E2:E12,A2:D12,TRUE,TRUE) |
Example 4 - Using the F and r2 Statistics
In the preceding example, the coefficient of determination, or r2, is 0.99675 (see cell A17 in the output for LINEST), which would indicate a strong relationship between the independent variables and the sale price. You can use the F statistic to determine whether these results, with such a high r2 value, occurred by chance.
Assume for the moment that in fact there is no relationship among the variables, but that you have drawn a rare sample of 11 office buildings that causes the statistical analysis to demonstrate a strong relationship. The term "Alpha" is used for the probability of erroneously concluding that there is a relationship.
The F and df values in output from the LINEST function can be used to assess the likelihood of a higher F value occurring by chance. F can be compared with critical values in published F-distribution tables or the FDIST function in Excel can be used to calculate the probability of a larger F value occurring by chance. The appropriate F distribution has v1 and v2 degrees of freedom. If n is the number of data points and const = TRUE or omitted, then v1 = n – df – 1 and v2 = df. (If const = FALSE, then v1 = n – df and v2 = df.) The FDIST function — with the syntax FDIST(F,v1,v2) — will return the probability of a higher F value occurring by chance. In this example, df = 6 (cell B18) and F = 459.753674 (cell A18).
Assuming an Alpha value of 0.05, v1 = 11 – 6 – 1 = 4 and v2 = 6, the critical level of F is 4.53. Since F = 459.753674 is much higher than 4.53, it is extremely unlikely that an F value this high occurred by chance. (With Alpha = 0.05, the hypothesis that there is no relationship between known_y’s and known_x’s is to be rejected when F exceeds the critical level, 4.53.) You can use the FDIST function in Excel to obtain the probability that an F value this high occurred by chance. For example, FDIST(459.753674, 4, 6) = 1.37E-7, an extremely small probability. You can conclude, either by finding the critical level of F in a table or by using the FDIST function, that the regression equation is useful in predicting the assessed value of office buildings in this area. Remember that it is critical to use the correct values of v1 and v2 that were computed in the preceding paragraph.
Example 5 - Calculating the t-Statistics
Another hypothesis test will determine whether each slope coefficient is useful in estimating the assessed value of an office building in Example 3. For example, to test the age coefficient for statistical significance, divide -234.24 (age slope coefficient) by 13.268 (the estimated standard error of age coefficients in cell A15). The following is the t-observed value:
t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7
If the absolute value of t is sufficiently high, it can be concluded that the slope coefficient is useful in estimating the assessed value of an office building in Example 3. The following table shows the absolute values of the 4 t-observed values.
If you consult a table in a statistics manual, you will find that t-critical, two tailed, with 6 degrees of freedom and Alpha = 0.05 is 2.447. This critical value can also be found by using the TINV function in Excel. TINV(0.05,6) = 2.447. Because the absolute value of t (17.7) is greater than 2.447, age is an important variable when estimating the assessed value of an office building. Each of the other independent variables can be tested for statistical significance in a similar manner. The following are the t-observed values for each of the independent variables.
|
Variable |
t-observed value |
|---|---|
|
Floor space |
5.1 |
|
Number of offices |
31.3 |
|
Number of entrances |
4.8 |
|
Age |
17.7 |
These values all have an absolute value greater than 2.447; therefore, all the variables used in the regression equation are useful in predicting the assessed value of office buildings in this area.










