Šioje temoje aptariamos skirtingos krypties linijos parinktys, pasiekiamos "Office".
Naudokite šio tipo krypties liniją, kad sukurtumėte geriausiai tinkančią tiesią liniją paprastiems linijinių duomenų rinkiniams. Jūsų duomenys yra tiesiniai, jei duomenų elementų modelis atrodo kaip linija. Linijinė krypties linija paprastai rodo, kad kas nors tolygiai didėja arba mažėja.
Linijinė krypties linija naudoja šią lygtį, kad apskaičiuotų mažiausius kvadratus, telpančius tiesei:
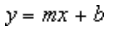
čia m yra krypties koeficientas, o b – ašis.
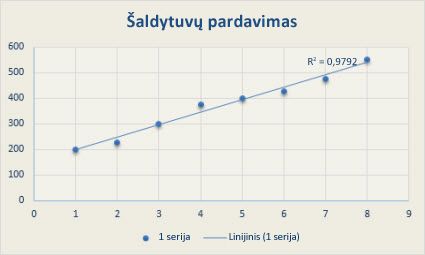
Toliau pateikta linijinė krypties linija rodo, kad šaldytuvų pardavimas nuolat didėjo per 8 metus. Atkreipkite dėmesį, kad R kvadratu apskliausta reikšmė (skaičius nuo 0 iki 1, rodanti, kaip artimai apskaičiuotos krypties linijos reikšmės atitinka faktinius duomenis) yra 0,9792, o tai gerai atitinka liniją duomenims.
Geriausiai tinkančio vingiuotos linijos rodymas, ši krypties linija yra naudinga, kai duomenų pokyčio greitis greitai didėja arba mažėja, o tada išsilygina. Logaritminė krypties linija gali naudoti neigiamas ir teigiamas reikšmes.
Logaritminė krypties linija naudoja šią lygtį, kad apskaičiuotų mažiausius kvadratus, telpančius per taškus:
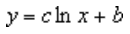
kur c ir b yra konstantos, ln yra natūrali logaritmo funkcija.
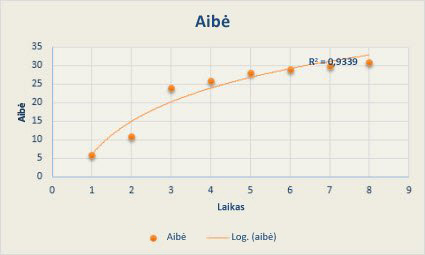
Toliau pateikta logaritminė krypties linija rodo prognozuojamą gyvūnų populiacijų augimą fiksuotoje erdvėje, kur gyventojų skaičius išsispręsdavo, nes sumažėjo gyvūnų erdvė. Atkreipkite dėmesį, kad R kvadratu reikšmė yra 0,933, o tai gana gerai atitinka liniją duomenims.
Ši krypties linija yra naudinga, kai duomenys kinta. Pavyzdžiui, kai analizuojate didelio duomenų rinkinio pelną ir nuostolius. Polinomo eilės tvarką galima nustatyti pagal duomenų svyravimų skaičių arba pagal tai, kiek posūkių (kalvos ir slėniai) atsiranda kreivėje. Paprastai 2-osios eilės polinomų krypties linija turi tik vieną kalvą ar slėnį, 3 užsakymas turi vieną arba dvi kalvas ar slėnius, o 4-ame užsakyme yra iki trijų kalvų ar slėnių.
Daugianarė arba curvilinear krypties linija naudoja šią lygtį, kad apskaičiuotų mažiausius kvadratus, telpančius per taškus:
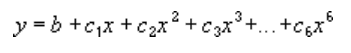
kur b ir 
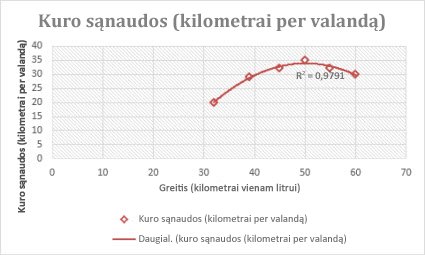
Ši 2 eilės daugianarė krypties linija (viena kalva) rodo ryšį tarp važiavimo greičio ir degalų sąnaudų. Atkreipkite dėmesį, kad R kvadratu reikšmė yra 0,979, kuri yra artima 1, kad linija gerai atitiktų duomenis.
Ši krypties linija rodoma lenkta linija, ji naudinga duomenų rinkiniams, kurie lygina matavimus, kurie didėja tam tikru greičiu. Pavyzdžiui, konkuratoriaus pagreitis 1 sekundės intervalais. Negalite sukurti maitinimo krypties linijos, jei jūsų duomenyse yra nulinių arba neigiamų reikšmių.
Energijos krypties linija naudoja šią lygtį, kad apskaičiuotų mažiausius kvadratus, telpančius per taškus:
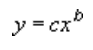
kur c ir b yra konstantos.
Pastaba: Ši parinktis negalima, kai jūsų duomenyse yra neigiamų arba nulinių reikšmių.
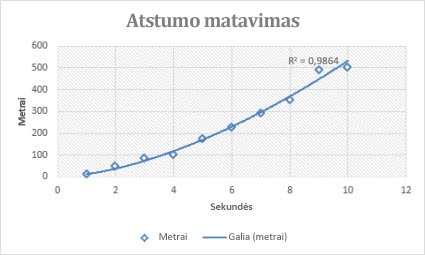
Toliau pateiktoje atstumo matavimo diagramoje atstumai rodomi metrais sekundėmis. Energijos krypties linija aiškiai rodo didėjantį spartinimą. Atkreipkite dėmesį, kad R kvadratu reikšmė yra 0,986, kuri beveik puikiai tinka linijai prie duomenų.
Ši krypties linija rodoma lenkta linija, kai duomenų reikšmės pakyla arba nukrenta nuolat didėjančiu greičiu. Eksponentinės krypties linijos sukurti negalima, jei jūsų duomenyse yra nulinių arba neigiamų reikšmių.
Eksponentinė krypties linija naudoja šią lygtį, kad apskaičiuotų mažiausius kvadratus, telpančius per taškus:
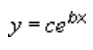
čia c ir b yra konstantos, o e – natūralaus logaritmo pagrindas.
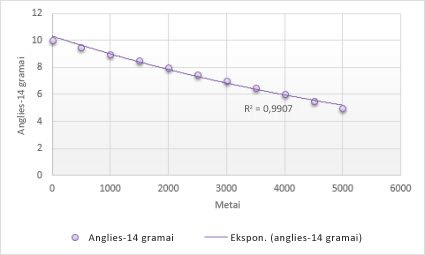
Toliau pateikta eksponentinė krypties linija rodo mažėjantį anglies 14 kiekį objekte, jam sulaukus amžiaus. Atkreipkite dėmesį, kad R kvadratu reikšmė yra 0,990, o tai reiškia, kad linija beveik puikiai tinka duomenims.
Ši krypties linija išlygiuoja duomenų svyravimus, kad būtų aiškiau pavaizduotas modelis ar tendencija. Slankusis vidurkis naudoja konkretų duomenų taškų skaičių (nustatytą pagal parinktį Laikotarpis ), juos apskaičiuoja ir naudoja vidutinę reikšmę kaip eilutės tašką. Pavyzdžiui, jei Periodas nustatytas kaip 2, pirmųjų dviejų duomenų taškų vidurkis naudojamas kaip pirmasis slankiojo vidurkio krypties linijos taškas. Antro ir trečio duomenų taškų vidurkis naudojamas kaip antras krypties linijos taškas ir t. t.
Slankiojo vidurkio krypties linija naudoja šią lygtį:
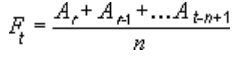
slankusis vidurkis krypties linijos taškų skaičius lygus bendram sekos taškų skaičiui atėmus nurodytą laikotarpio skaičių.
Sklaidos diagramoje krypties linija pagrįsta x reikšmių tvarka diagramoje. Kad būtų geresnis rezultatas, rūšiuokite x reikšmes prieš įtraukdami slankųjį vidurkį.
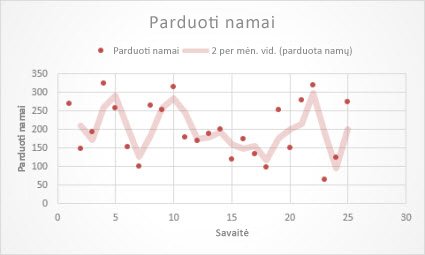
Toliau pateikta slankiojo vidurkio krypties linija rodo per 26 savaites parduotų namų skaičių.
Svarbu: Pradedant nuo 2005 m. "Excel" versijos, "Excel" koreguota taip, kaip ji skaičiuoja linijinės krypties linijų reikšmę R2 diagramose, kurių krypties linijos ašis nustatyta kaip nulis (0). Šis koregavimas taiso skaičiavimus, kurie pateikė neteisingas R2 reikšmes, ir lygiuoja R2 skaičiavimą su funkcija LINEST. Todėl diagramose, anksčiau sukurtose ankstesnėse "Excel" versijose, gali būti rodomos skirtingos R2 reikšmės. Daugiau informacijos žr. Vidinių linijinių krypties linijų diagramoje skaičiavimo pakeitimai.
Reikia daugiau pagalbos?
Visada galite paklausti „Excel“ technologijų bendruomenės specialisto arba gauti palaikymo bendruomenėse.
Taip pat žr.
Krypties arba slankiojo vidurkio linijos įtraukimas į diagramą










