LINEST 関数

説明

LINEST 関数は、"最小二乗法" を使って指定したデータに最もよく適合する直線を算出し、この直線を記述する配列を返すことによって直線の補正項を計算します。 LINEST 関数を他の関数と共に使用して、多項式近似、対数近似、指数近似、べき級数をはじめとする、不明なパラメーター内で線形近似を示す他の種類のモデルの統計を計算することもできます。 この関数は値の配列を返すため、配列数式として入力する必要があります。 方法については、この記事の「使用例」の後に示します。

直線は次の方程式で表されます。

y = mx + b

または

y = m1x1 + m2x2 + ... + b

これは、x の値が複数の範囲にある場合に適用されます (ここで、従属変数 y は独立変数 x の関数です)。 m の値はそれぞれの x の値に対応する係数であり、b は定数です。 y、x、および m がベクトル (1 次元配列) であり得ることに注意してください。 LINEST 関数が返す配列は、{mn,mn-1,...,m1,b} となります。 また、回帰直線の補正項も追加情報として返されます。

書式

LINEST(既知の y, [既知の x], [定数], [補正])

LINEST 関数の書式には、次の引数があります。

構文

• 既知の y    必ず指定します。 既にわかっている y の値の系列であり、y = mx + b という関係が成り立ちます。

  • "既知の y" の配列が 1 つの列に入力されている場合、"既知の x" の各列はそれぞれ異なる変数であると見なされます。

  • "既知の y" の配列が 1 つの行に入力されている場合、"既知の x" の各行はそれぞれ異なる変数であると見なされます。

• 既知の x    省略可能です。 既にわかっている x の値の系列であり、y = mx + b という関係が成り立ちます。

  • "既知の x" の配列には、1 つまたは複数の変数の系列を指定できます。 変数の系列が 1 つである場合、既知の y と既知の x は、それぞれの次元が同じであれば、どのような形の範囲であってもかまいません。 変数の系列が複数である場合、既知の y はベクトル (高さが 1 行、または幅が 1 列のセル範囲) でなければなりません。

  • 既知の x を省略すると、既知の y と同じサイズの {1,2,3...} という配列を指定したと見なされます。

• 定数    省略可能です。 定数 b を 0 にするかどうかを論理値で指定します。

  • 定数 を TRUE に設定するか省略すると、b の値も計算されます。

  • "定数" に FALSE を指定すると、b の値が 0 に設定され、y = mx となるように m の値が調整されます。

• 補正    省略可能です。 回帰直線の補正項を追加情報として返すかどうかを論理値で指定します。

  • "補正"にTRUEを指定すると、回帰直線の補正項が返され、返される配列は {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid} となります。

  • "補正"にFALSEを指定するか省略すると、m 係数と定数 b のみが返されます。

    次のような回帰直線の補正項が追加情報として返されます。

次の図は、回帰直線の追加の補正項が返される順序を示します。

解説

• 傾きと y 切片を使って任意の直線を記述できます。

  傾き (m):
  直線の傾き (m) は、直線上の 2 点の座標が (x1,y1)、(x2,y2) で表されるとき、(y2 - y1)/(x2 - x1) で計算できます。

  y 切片 (b):
  直線の y 切片 (b) とは、直線が y 軸と交わるときの y の値です。

  直線の方程式は y = mx + b で表されます。 m と b の値がわかれば、y または x の値をこの方程式に代入して、直線上の任意の点の座標を計算できます。 この計算に、TREND 関数を使用することもできます。

• 独立変数 x が 1 つしかわからないときは、次の数式を使用すると、傾きと y 切片を計算することができます。

  傾き:
  =INDEX(LINEST(既知の y,既知の x),1)

  y 切片:
  =INDEX(LINEST(既知の y,既知の x),2)

• LINEST 関数で計算した直線の精度は、指定したデータのばらつきによって決まります。 データの分布がより直線に近ければ、LINEST 関数のモデルの精度はそれだけ向上します。 LINEST 関数では、データに最もよく合う直線を見つけるために最小二乗法を使用しています。 独立変数 x の値が 1 つしかわからないときは、次の数式を使って m と b の値が計算されます。

  

  

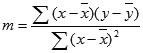
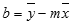
  ここで、x は標本平均 "AVERAGE(既知の x)"、y は標本平均 "AVERAGE(既知の y)" です。

• 直線/曲線調整関数のLINESTとLOGEST関数は、データに適した最適な直線または指数曲線を計算できます。 ただし、どちらの結果がデータに最適かを判断する必要があります。 直線の傾向 (既知の y, 既知の y)を計算し、指数曲線の場合はGROWTH (既知の y, 既知のy)を計算することができます。 これらの関数は、"新しい x " 引数を指定せずに、その直線または曲線に沿って実際のデータポイントで予測される y 値の配列を返します。 これにより、予測される値を実際の値と比較することができます。 視覚的に比較できるように、両方をグラフ化することもできます。

• 回帰分析では、直線上の各点ごとに、予測される y の値と実際の y の値との平方差が計算されます。 このようにして計算した平方差の合計を "残余の平方和" (ssresid) と呼びます。 次に、"総平方和" (sstotal) が計算されます。 "定数" に TRUE を指定するか省略すると、総平方和は、実際の y の値と y の平均値の平方差の合計となります。 "定数" に FALSE を指定すると、総平方和は、(個々の y の値から y の平均値を引いたものではなく) 実際の y の値の平方和となります。 回帰の平方和 ssreg は、ssreg = sstotal - ssresid として計算されます。 総平方和と比較し、残余の平方和が小さければ小さいほど、確実度の係数である r2 の値が大きくなり、回帰分析で得られた方程式が変数間の関係をより正確に表していることになります。 ここで、r2 = ssreg/sstotal です。

• 場合によっては、X 列が1つまたは複数 (列に含まれていることを前提としています)、その他の X 列の存在に、追加の予測値が存在しないことがあります。 つまり、1つまたは複数の X 列を除外すると、予測される Y 値の予測値が同じになることがあります。 その場合、これらの冗長な X 列は回帰モデルから省略する必要があります。 この現象は "共線性" と呼ばれます。冗長な X 列は、非冗長な X 列の倍数の合計として表すことができます。 LINEST関数は、共線性をチェックし、それらを識別するときに回帰モデルから余分な X 列を削除します。 削除された X 列は、0の係数に加えて0係数を持つため、 LINESTの出力で認識できます。 1つ以上の列が冗長として削除された場合、df は予測目的で実際に使用されている X 列の数に依存するため、df が影響を受けます。 Df の計算の詳細については、「例 4」を参照してください。 Df が変更されたために、重複する X 列が削除されるため、sey と F の値も影響を受けます。 共線性は、実際にはあまり一般的ではありません。 ただし、1つの例としては、一部の X 列に0と1の値しか含まれていない場合、実験の件名が特定のグループのメンバーでないかどうかを示すインジケーターとして表示されることがあります。 定数= TRUE または省略した場合、 LINEST関数は、切片をモデル化するために、すべての1つの値について追加の X 列を効果的に挿入します。 男性の場合は各項目に1つの列があり、それ以外の場合は0の場合は "女性" の場合は "1"、"0 の場合は" 0、そうでない場合は "男性インジケータ" のエントリを減算することで、その列は冗長になります。LINEST関数によって追加されたすべての1つの値の追加列のエントリの列。

• 次のように、df の値が計算されます。このとき、"既知の X" と " const = TRUE" または "false" のように、k 列が含まれている場合は、df = n – k –1という値が表示されます。 定数= FALSE、df = n-k どちらの場合も、共線性によって削除された各 X 列は、df の値が1ずつ増加します。

• 計算結果が配列となる数式は、配列数式として入力する必要があります。

  注: Excel Online 配列数式を作成することはできません。

• "既知の x" などで引数に配列定数を指定するとき、同じ行の値を区切るには半角のコンマ (,) を使い、各行を区切るには半角のセミコロン (;) を使います。 区切り記号は、地域設定によって異なる場合があります。

• 回帰方程式によって予測計算された y の値が、方程式を決定するときに使用した y の値の範囲では、適切な値にならない場合があります。

• LINEST 関数の基になるアルゴリズムは、SLOPE 関数や INTERCEPT 関数の基になるアルゴリズムとは異なります。 そのため、データが不定で共線性がある場合に、結果が異なることがあります。 たとえば、"既知の y" 引数のデータ要素が 0、"既知の x" 引数のデータ要素が 1 の場合、次のような動作になります。

  • LINEST 関数では値 0 が返されます。 "LINEST" のアルゴリズムでは、共線性があるデータに対して適切な結果を返すようになっており、この場合は少なくとも 1 つの答えが見つかります。

  • SLOPE 関数と INTERCEPT 関数では、エラー #DIV/0! が返されます。 SLOPE 関数と INTERCEPT 関数のアルゴリズムは唯一の答えを見つけるようになっており、この場合は複数の答えがあり得ます。

• LOGEST を使用して他の種類の回帰分析の統計を計算することに加えて、LINEST を使用すると、x 変数と y 変数の関数を LINEST の x 系列と y 系列として入力することによって、他の一連の回帰分析を計算できます。 例として、次の数式を参照してください。

  =LINEST(yvalues, xvalues^COLUMN($A:$C))

  この数式では、単一列の x 値と y 値を使用して、次の形式の立方体 (3 次多項式) の近似値を計算できます。

  y = m1*x + m2*x^2 + m3*x^3 + b

  この式を調整することによって、他の種類の回帰分析を計算できますが、出力値およびその他の統計値の調整が必要になる場合もあります。

• LINEST 関数から返される F 検定の値は、FTEST 関数から返される F 検定の値と異なります。 LINEST 関数は F 補正項を返し、FTEST 関数は確率を返します。

使用例