Come può una società utilizzare il Risolutore per determinare quali progetti deve intraprendere?
Ogni anno, una società come Eli Lilly deve determinare quali farmaci sviluppare; una società come Microsoft, quali programmi software sviluppare; una società come Proctor & Gamble, che sviluppa nuovi prodotti di consumo. La funzionalità Risolutore di Excel consente a un'azienda di prendere queste decisioni.
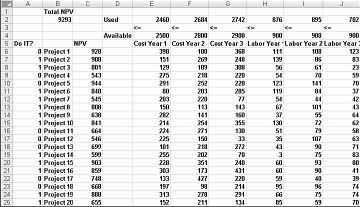
La maggior parte delle società desidera intraprendere progetti che contribuiscono al massimo valore attuale netto (VAN), soggetti a risorse limitate (in genere capitale e manodopera). Si supponga che una società di sviluppo di software stia cercando di determinare quali dei 20 progetti software deve intraprendere. La funzione VAN (in milioni di dollari) fornita da ogni progetto, nonché la capitale (in milioni di dollari) e il numero di programmatori necessari per ognuno dei tre anni successivi sono indicati nel foglio di lavoro Modello base nel file Capbudget.xlsx, come illustrato nella figura 30-1 della pagina successiva. Ad esempio, Project 2 restituisce $ 908 milioni. Richiede 151 milioni di dollari durante l'anno 1, $ 269 milioni durante l'anno 2 e $ 248 milioni durante l'anno 3. Project 2 richiede 139 programmatori durante l'anno 1, 86 programmatori durante l'anno 2 e 83 programmatori durante l'anno 3. Le celle E4:G4 mostrano la capitale (in milioni di dollari) disponibile durante ognuno dei tre anni e le celle H4:J4 indicano quanti programmatori sono disponibili. Ad esempio, durante l'anno 1 fino a $ 2,5 miliardi di capitale e 900 programmatori sono disponibili.
La società deve decidere se intraprendere ciascun progetto. Supponiamo che non possiamo intraprendere una frazione di un progetto software; se allochiamo 0,5 delle risorse necessarie, ad esempio, avremmo un programma non lavorativo che ci porterà $ 0 ricavi!
Il trucco nelle situazioni di modellazione in cui si fa o non si fa qualcosa è usare celle binarie variabili. Una cella binaria che cambia è sempre uguale a 0 o 1. Quando una cella binaria variabile che corrisponde a un progetto è uguale a 1, il progetto viene eseguito. Se una cella binaria variabile che corrisponde a un progetto è uguale a 0, il progetto non viene eseguito. È possibile configurare il Risolutore in modo da usare un intervallo di celle binarie variabili aggiungendo un vincolo. Selezionare le celle variabili da usare e quindi scegliere Bin dall'elenco nella finestra di dialogo Aggiungi vincolo.
Con questo sfondo, siamo pronti a risolvere il problema di selezione del progetto software. Come sempre con un modello Risolutore, si inizia identificando la cella di destinazione, le celle variabili e i vincoli.
-
Cella di destinazione. La funzione VAN generata dai progetti selezionati viene ingrandita.
-
Celle variabili. Cerchiamo una cella di modifica binaria 0 o 1 per ogni progetto. Ho individuato queste celle nell'intervallo A6:A25 e ho chiamato l'intervallo doit. Ad esempio, un 1 nella cella A6 indica che Microsoft ha intrapreso il progetto 1; 0 nella cella C6 indica che non è possibile intraprendere il Progetto 1.
-
Vincoli. È necessario assicurarsi che per ogni anno t (t=1, 2, 3), il capitale di anno t utilizzato sia minore o uguale al capitale t dell'anno disponibile e il lavoro anno t usato sia minore o uguale al lavoro t anno disponibile.
Come si può vedere, il foglio di lavoro deve calcolare per qualsiasi selezione di progetti la van, il capitale utilizzato annualmente e i programmatori utilizzati ogni anno. Nella cella B2 si usa la formula MATR.SOMMA.PRODOTTO(doit;VAN) per calcolare il totale della van generata dai progetti selezionati. Il nome van dell'intervallo fa riferimento all'intervallo C6:C25. Per ogni progetto con uno 1 nella colonna A, questa formula preleva la van del progetto e per ogni progetto con uno 0 nella colonna A, questa formula non preleva la van del progetto. Di conseguenza, è possibile calcolare la funzione VAN di tutti i progetti e la cella di destinazione è lineare perché viene calcolata sommando i termini che seguono la maschera (cella variabile)*(costante). In modo analogo, calcolo il capitale utilizzato ogni anno e il lavoro usato ogni anno copiando da E2 a F2:J2 la formula MATR.SOMMA.PRODOTTO(doit;E6:E25).
Ora inserisco la finestra di dialogo Parametri Risolutore, come illustrato nella figura 30-2.
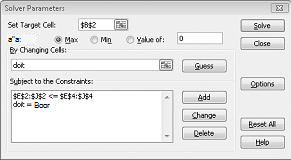
Il nostro obiettivo è massimizzare la van dei progetti selezionati (cella B2). Le celle variabili (l'intervallo denominato doit) sono le celle binarie variabili per ogni progetto. Il vincolo E2:J2<=E4:J4 assicura che durante ogni anno il capitale e la manodopera utilizzati siano inferiori o uguali al capitale e al lavoro disponibili. Per aggiungere il vincolo che rende binarie le celle variabili, faccio clic su Aggiungi nella finestra di dialogo Parametri Risolutore e quindi seleziono Bin nell'elenco al centro della finestra di dialogo. La finestra di dialogo Aggiungi vincolo dovrebbe essere visualizzata come illustrato nella figura 30-3.
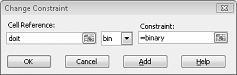
Il modello è lineare perché la cella di destinazione viene calcolata come somma dei termini che contengono la maschera (cella variabile)*(costante) e perché i vincoli di utilizzo delle risorse vengono calcolati confrontando la somma di (celle variabili)*(costanti) con una costante.
Con la finestra di dialogo Parametri Risolutore compilata, fare clic su Risolvi per visualizzare i risultati illustrati in precedenza nella figura 30-1. La società può ottenere un van massimo di $ 9.293 milioni ($ 9,293 miliardi) scegliendo Progetti 2, 3, 6-10, 14-16, 19 e 20.
A volte i modelli di selezione del progetto hanno altri vincoli. Si supponga, ad esempio, che se si seleziona Progetto 3 sia necessario selezionare anche Progetto 4. Poiché la soluzione ottimale corrente seleziona Project 3 ma non Project 4, sappiamo che la soluzione corrente non può rimanere ottimale. Per risolvere questo problema, aggiungere semplicemente il vincolo che la cella binaria modifica per Project 3 è minore o uguale alla cella binaria di modifica per Project 4.
Questo esempio è disponibile nel foglio di lavoro If 3 then 4 nel file Capbudget.xlsx, come illustrato nella figura 30-4. La cella L9 fa riferimento al valore binario correlato a Project 3 e alla cella L12 al valore binario correlato a Project 4. Aggiungendo il vincolo L9<=L12, se si sceglie Progetto 3, L9 è uguale a 1 e il vincolo forza L12 (il binario di Project 4) a essere uguale a 1. Il vincolo deve inoltre lasciare senza restrizioni il valore binario nella cella modificabile di Project 4 se non si seleziona Project 3. Se non si seleziona Progetto 3, L9 è uguale a 0 e il vincolo consente al binario di Project 4 di essere uguale a 0 o 1, che è ciò che si vuole. La nuova soluzione ottimale è illustrata nella figura 30-4.
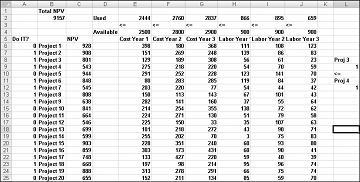
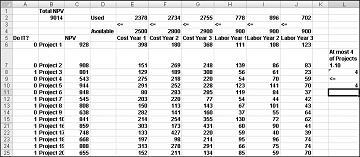
Una nuova soluzione ottimale viene calcolata se si seleziona Project 3 significa che è necessario selezionare anche Project 4. Si supponga di poter eseguire solo quattro progetti compresi tra i progetti da 1 a 10. Vedere il foglio di lavoro Al massimo 4 di P1-P10 , illustrato nella figura 30-5. Nella cella L8 la somma dei valori binari associati ai progetti da 1 a 10 viene calcolata con la formula SOMMA(A6:A15). Quindi si aggiunge il vincolo L8<=L10, che assicura che vengano selezionati al massimo 4 dei primi 10 progetti. La nuova soluzione ottimale è illustrata nella figura 30-5. La van è scesa a $ 9,014 miliardi.
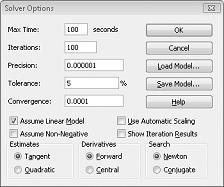
I modelli del Risolutore lineare in cui alcune o tutte le celle variabili sono necessarie per essere binarie o integer sono in genere più difficili da risolvere rispetto ai modelli lineari in cui tutte le celle variabili possono essere frazioni. Per questo motivo, spesso siamo soddisfatti di una soluzione quasi ottimale a un problema di programmazione binario o intero. Se il modello del Risolutore viene eseguito per molto tempo, è consigliabile modificare l'impostazione Tolleranza nella finestra di dialogo Opzioni Risolutore. Vedere la figura 30-6. Ad esempio, un'impostazione Tolleranza pari a 0,5% indica che il Risolutore interromperà la prima volta che trova una soluzione fattibile entro lo 0,5% del valore teorico ottimale della cella di destinazione (il valore teorico ottimale della cella di destinazione è il valore target ottimale trovato quando vengono omessi i vincoli binari e interi). Spesso ci troviamo di fronte a una scelta tra trovare una risposta entro il 10% di ottimale in 10 minuti o trovare una soluzione ottimale in due settimane di tempo al computer! Il valore di tolleranza predefinito è 0,05%, il che significa che il Risolutore si interrompe quando trova un valore di cella di destinazione entro lo 0,05% del valore teorico ottimale della cella di destinazione.
-
Una società ha nove progetti in esame. La funzione VAN aggiunta da ogni progetto e il capitale richiesto da ogni progetto nei due anni successivi sono illustrati nella tabella seguente. Tutti i numeri sono in milioni. Ad esempio, il progetto 1 aggiungerà 14 milioni di euro in VAN e richiederà spese di $ 12 milioni durante l'anno 1 e $ 3 milioni durante l'anno 2. Nel corso dell'anno 1, sono disponibili 50 milioni di dollari di capitale per i progetti e 20 milioni di dollari durante l'anno 2.
|
VAN |
Spese anno 1 |
Spese anno 2 |
|
|---|---|---|---|
|
Progetto 1 |
14 |
12 |
3 |
|
Progetto 2 |
17 |
54 |
7 |
|
Project 3 |
17 |
6 |
6 |
|
Project 4 |
15 |
6 |
2 |
|
Project 5 |
40 |
30 |
35 |
|
Project 6 |
12 |
6 |
6 |
|
Project 7 |
14 |
48 |
4 |
|
Progetto 8 |
10 |
36 |
3 |
|
Progetto 9 |
12 |
18 |
3 |
-
Se non è possibile intraprendere una frazione di un progetto ma è necessario eseguire un progetto, tutto o nessuno, come è possibile massimizzare van?
-
Si supponga che, se si esegue il Progetto 4, è necessario intraprendere il Progetto 5. Come è possibile massimizzare la funzione VAN?
-
Una casa editrice sta cercando di determinare quale dei 36 libri dovrebbe pubblicare quest'anno. Il file Pressdata.xlsx fornisce le seguenti informazioni su ogni libro:
-
Ricavi previsti e costi di sviluppo (in migliaia di dollari)
-
Pagine in ogni libro
-
Se il libro è orientato verso un pubblico di sviluppatori di software (indicato da un 1 nella colonna E)
Una società di pubblicazione può pubblicare libri per un totale di 8500 pagine quest'anno e deve pubblicare almeno quattro libri destinati agli sviluppatori di software. In che modo l'azienda può massimizzare il suo profitto?
-
Questo articolo è stato adattato da Wayne L. Winston in Microsoft Office Excel 2007 Data Analysis and Business Modeling .
Questo libro in stile classroom è stato sviluppato da una serie di presentazioni di Wayne Winston, un noto statistico e professore d'affari specializzato in applicazioni creative e pratiche di Excel.










