Nota: Riteniamo importante fornire il contenuto della Guida più recente non appena possibile, nella lingua dell'utente. Questa pagina è stata tradotta automaticamente e potrebbe contenere errori di grammatica o imprecisioni. L'intento è quello di rendere fruibile il contenuto. Nella parte inferiore della pagina è possibile indicare se le informazioni sono risultate utili. Questo è l' articolo in lingua inglese per riferimento.
Restituisce la distribuzione ipergeometrica. DISTRIB.IPERGEOM restituisce la probabilità di un dato numero di successi di un campione in base alla dimensione del campione, ai successi e alla dimensione della popolazione. Utilizzare la funzione DISTRIB.IPERGEOM per risolvere i problemi relativi all'analisi di una popolazione limitata, dove ciascuna osservazione può essere tanto un successo quanto un insuccesso e dove ciascun sottoinsieme di una data dimensione viene scelto con uguale probabilità.
Sintassi
DISTRIB.IPERGEOM(s_esempio;num_esempio;s_pop;num_pop)
S_esempio è il numero di successi nel campione.
Num_esempio è la dimensione del campione.
S_pop è il numero di successi nella popolazione.
Num_pop Dimensione della popolazione.
Osservazioni
-
La parte decimale di tutti gli argomenti viene troncata.
-
Se qualsiasi argomento non è numerico, DISTRIB.IPERGEOM restituirà il valore di errore #VALORE!.
-
Se s_esempio < 0 o s_esempio è maggiore del valore minore di num_esempio o s_pop, DISTRIB.IPERGEOM restituirà il valore di errore #NUM!.
-
Se s_esempio è minore del valore maggiore rispetto a 0 o di (num_esempio - num_pop + s_pop), DISTRIB.IPERGEOM restituirà il valore di errore #NUM!.
-
Se num_esempio è < 0 o > num_pop, DISTRIB.IPERGEOM restituirà il valore di errore #NUM!.
-
Se s_pop è < 0 o > num_pop, DISTRIB.IPERGEOM restituirà il valore di errore #NUM!.
-
Se num_pop è < 0, DISTRIB.IPERGEOM restituirà il valore di errore #NUM!.
-
Per la distribuzione ipergeometrica viene utilizzata l'equazione seguente:
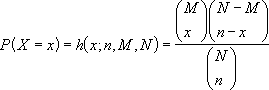
dove:
x = s_esempio
n = num_esempio
M = s_pop
N = num_pop
La funzione DISTRIB.IPERGEOM viene utilizzata per campionare una popolazione limitata senza effettuare sostituzioni.
Esempio
Una scatola contiene 20 cioccolatini. Otto cioccolatini sono al liquore e i rimanenti 12 sono alle noci. Se una persona sceglie quattro cioccolatini a caso, sarà possibile utilizzare la seguente funzione per calcolare la probabilità che un solo cioccolatino sia al liquore.
|
S_esempio |
Num_esempio |
S_pop |
Num_pop |
Formula |
Descrizione (risultato) |
|
1 |
4 |
8 |
20 |
=DISTRIB.IPERGEOM([S_esempio];[Num_esempio];[S_pop];[Num_pop]) |
Distribuzione ipergeometrica di campione e popolazione (0,363261) |










