Bagaimana perusahaan dapat menggunakan Solver untuk menentukan proyek mana yang harus dikerjakannya?
Setiap tahun, perusahaan seperti Eli Lilly perlu menentukan obat mana yang akan dikembangkan; perusahaan seperti Microsoft, program perangkat lunak mana yang akan dikembangkan; perusahaan seperti Proctor & Gamble, yang produk konsumen baru untuk dikembangkan. Fitur Solver di Excel bisa membantu perusahaan membuat keputusan ini.
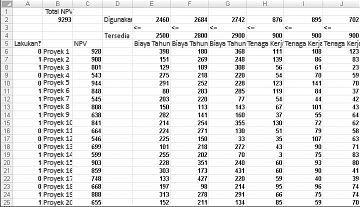
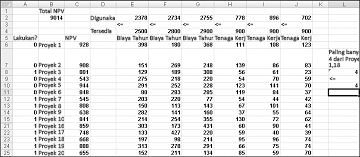
Sebagian besar perusahaan ingin melakukan proyek yang menyumbang nilai bersih saat ini (NPV) terbesar, tunduk pada sumber daya terbatas (biasanya modal dan tenaga kerja). Katakanlah perusahaan pengembangan perangkat lunak mencoba menentukan mana dari 20 proyek perangkat lunak yang harus dilakukannya. NPV (dalam jutaan dolar) disumbang oleh setiap proyek serta modal (dalam jutaan dolar) dan jumlah programmer yang diperlukan selama masing-masing tiga tahun ke depan diberikan pada lembar kerja Model Dasar dalam file Capbudget.xlsx, yang diperlihatkan dalam Gambar 30-1 di halaman berikutnya. Misalnya, Project 2 menghasilkan $908 juta. Ini membutuhkan $ 151 juta selama Tahun 1, $ 269 juta selama Tahun 2, dan $ 248 juta selama Tahun 3. Project 2 memerlukan 139 programmer selama Tahun 1, 86 programmer selama Tahun 2, dan 83 programmer selama Tahun 3. Sel E4:G4 memperlihatkan modal (dalam jutaan dolar) yang tersedia selama masing-masing dari tiga tahun, dan sel H4:J4 menunjukkan berapa banyak programmer yang tersedia. Misalnya, selama Tahun 1 hingga $2,5 miliar modal dan tersedia 900 programmer.
Perusahaan harus memutuskan apakah harus melakukan setiap proyek. Mari kita asumsikan bahwa kita tidak dapat melakukan sebagian kecil proyek perangkat lunak; jika kita mengalokasikan 0,5 dari sumber daya yang diperlukan, misalnya, kita akan memiliki program non-kerja yang akan membawa kita $0 pendapatan!
Trik dalam situasi pemodelan di mana Anda melakukan atau tidak melakukan sesuatu adalah menggunakan sel perubahan biner. Sel yang berubah biner selalu sama dengan 0 atau 1. Ketika sel pengubahan biner yang terkait dengan proyek sama dengan 1, kami melakukan proyek. Jika sel pengubahan biner yang terkait dengan proyek sama dengan 0, kami tidak melakukan proyek. Anda menyiapkan Solver untuk menggunakan rentang sel pengubah biner dengan menambahkan batasan—pilih sel yang berubah yang ingin Anda gunakan lalu pilih Biner dari daftar dalam kotak dialog Tambahkan Batasan.
Dengan latar belakang ini, kami siap untuk menyelesaikan masalah pemilihan proyek perangkat lunak. Seperti biasa dengan model Solver, kita mulai dengan mengidentifikasi sel target, sel yang berubah, dan batasan.
-
Sel target. Kami memaksimalkan NPV yang dihasilkan oleh proyek yang dipilih.
-
Mengubah sel. Kami mencari sel biner mengubah 0 atau 1 untuk setiap proyek. Saya telah menemukan sel-sel ini di rentang A6:A25 (dan menamai rentang doit). Misalnya, 1 dalam sel A6 menunjukkan bahwa kami melakukan Project 1; 0 dalam sel C6 menunjukkan bahwa kami tidak melakukan Project 1.
-
Kendala. Kami perlu memastikan bahwa untuk setiap Tahun t (t=1, 2, 3), Modal tahun t yang digunakan kurang dari atau sama dengan tahun modal t yang tersedia, dan Tahun t tenaga kerja yang digunakan kurang dari atau sama dengan Tahun t tenaga kerja yang tersedia.
Seperti yang dapat Anda lihat, lembar kerja kami harus menghitung untuk setiap pilihan proyek NPV, modal yang digunakan setiap tahun, dan programmer yang digunakan setiap tahun. Di sel B2, saya menggunakan rumus SUMPRODUCT(doit,NPV) untuk menghitung total NPV yang dihasilkan oleh proyek yang dipilih. (Nama rentang NPV merujuk ke rentang C6:C25.) Untuk setiap proyek dengan 1 di kolom A, rumus ini mengambil NPV proyek, dan untuk setiap proyek dengan 0 di kolom A, rumus ini tidak mengambil NPV proyek. Oleh karena itu, kami dapat menghitung NPV dari semua proyek, dan sel target kami linear karena dihitung dengan menjumlahkan istilah yang mengikuti formulir (mengubah sel)*(konstanta). Dengan cara yang sama, saya menghitung modal yang digunakan setiap tahun dan tenaga kerja yang digunakan setiap tahun dengan menyalin dari E2 ke F2:J2 rumus SUMPRODUCT(doit,E6:E25).
Saya sekarang mengisi kotak dialog Parameter Solver seperti yang diperlihatkan dalam Gambar 30-2.
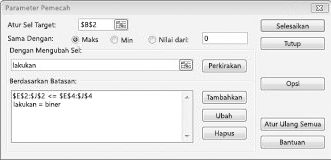
Tujuan kami adalah untuk memaksimalkan NPV proyek yang dipilih (sel B2). Sel kami yang berubah (rentang bernama doit) adalah sel biner yang berubah untuk setiap proyek. Batasan E2:J2<=E4:J4 memastikan bahwa selama setiap tahun modal dan tenaga kerja yang digunakan kurang dari atau sama dengan modal dan tenaga kerja yang tersedia. Untuk menambahkan batasan yang membuat sel berubah biner, saya klik Tambahkan dalam kotak dialog Parameter Solver lalu pilih Biner dari daftar di tengah kotak dialog. Kotak dialog Tambahkan Batasan akan muncul seperti yang diperlihatkan dalam Gambar 30-3.
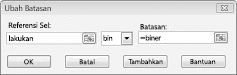
Model kami linear karena sel target dihitung sebagai jumlah istilah yang memiliki formulir (mengubah sel)*(konstanta) dan karena batasan penggunaan sumber daya dihitung dengan membandingkan jumlah (mengubah sel)*(konstanta) dengan konstanta .
Dengan kotak dialog Parameter Solver yang diisi, klik Selesaikan dan kami memiliki hasil yang diperlihatkan sebelumnya dalam Gambar 30-1. Perusahaan dapat memperoleh NPV maksimum $9,293 juta ($9,293 miliar) dengan memilih Projects 2, 3, 6–10, 14–16, 19, dan 20.
Terkadang model pemilihan proyek memiliki batasan lain. Misalnya, jika memilih Project 3, kita juga harus memilih Project 4. Karena solusi optimal kami saat ini memilih Project 3 tetapi bukan Project 4, kami tahu bahwa solusi kami saat ini tidak dapat tetap optimal. Untuk mengatasi masalah ini, cukup tambahkan batasan bahwa sel pengubahan biner untuk Project 3 kurang dari atau sama dengan sel perubahan biner untuk Project 4.
Anda bisa menemukan contoh ini pada lembar kerja If 3 lalu 4 dalam file Capbudget.xlsx, yang diperlihatkan dalam Gambar 30-4. Sel L9 merujuk ke nilai biner yang terkait dengan Project 3, dan sel L12 ke nilai biner yang terkait dengan Project 4. Dengan menambahkan batasan L9<=L12, jika kita memilih Project 3, L9 sama dengan 1 dan batasan kita memaksa L12 (biner Project 4) untuk sama dengan 1. Batasan kami juga harus membiarkan nilai biner dalam sel project 4 yang berubah tidak dibatasi jika kami tidak memilih Project 3. Jika kami tidak memilih Project 3, L9 sama dengan 0 dan batasan kami memungkinkan biner Project 4 sama dengan 0 atau 1, itulah yang kami inginkan. Solusi optimal baru diperlihatkan dalam Gambar 30-4.
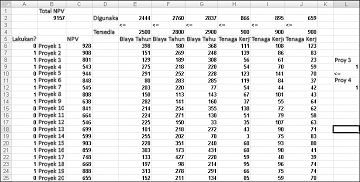
Solusi optimal baru dihitung jika memilih Project 3 berarti kita juga harus memilih Project 4. Sekarang anggaplah bahwa kita hanya bisa melakukan empat proyek dari antara Proyek 1 sampai 10. (Lihat Lembar kerja P1-P10 Paling Banyak 4 , diperlihatkan dalam Gambar 30-5.) Di sel L8, kami menghitung jumlah nilai biner yang terkait dengan Projects 1 sampai 10 dengan rumus SUM(A6:A15). Lalu kami menambahkan batasan L8<=L10, yang memastikan bahwa, paling banyak, 4 dari 10 proyek pertama dipilih. Solusi optimal baru diperlihatkan dalam Gambar 30-5. NPV telah turun menjadi $ 9,014 miliar.
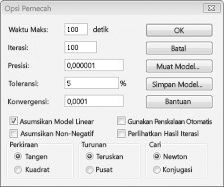
Model Solver Linear di mana beberapa atau semua sel yang berubah harus berupa biner atau bilangan bulat biasanya lebih sulit untuk dipecahkan daripada model linear di mana semua sel yang berubah diperbolehkan menjadi pecahan. Untuk alasan ini, kami sering puas dengan solusi yang hampir optimal untuk masalah pemrograman biner atau bilangan bulat. Jika model Solver Anda berjalan untuk waktu yang lama, Anda mungkin ingin mempertimbangkan untuk menyesuaikan pengaturan Toleransi dalam kotak dialog Opsi Solver. (Lihat Gambar 30-6.) Misalnya, pengaturan Toleransi 0,5% berarti solver akan berhenti saat pertama kali menemukan solusi yang layak yang berada dalam 0,5 persen dari nilai sel target optimal teoritis (nilai sel target optimal teoritis adalah nilai target optimal yang ditemukan ketika batasan biner dan bilangan bulat dihilangkan). Seringkali kita dihadapkan dengan pilihan antara menemukan jawaban dalam 10 persen dari optimal dalam 10 menit atau menemukan solusi optimal dalam dua minggu waktu komputer! Nilai Toleransi default adalah 0,05%, yang berarti Bahwa Solver berhenti ketika menemukan nilai sel Target dalam 0,05 persen dari nilai sel target optimal teoritis.
-
Perusahaan memiliki sembilan proyek di bawah pertimbangan. NPV yang ditambahkan oleh setiap proyek dan modal yang diperlukan oleh setiap proyek selama dua tahun ke depan diperlihatkan dalam tabel berikut. (Semua angka berada dalam jutaan.) Misalnya, Project 1 akan menambahkan $14 juta dalam NPV dan memerlukan pengeluaran sebesar $12 juta selama Tahun 1 dan $3 juta selama Tahun 2. Selama Tahun 1, modal $50 juta tersedia untuk proyek, dan $20 juta tersedia selama Tahun 2.
|
NPV |
Pengeluaran Tahun 1 |
Pengeluaran Tahun 2 |
|
|---|---|---|---|
|
Project 1 |
14 |
1.2 |
3 |
|
Project 2 |
17 |
54 |
7 |
|
Project 3 |
17 |
6 |
6 |
|
Project 4 |
15 |
6 |
2 |
|
Project 5 |
40 |
30 |
35 |
|
Project 6 |
1.2 |
6 |
6 |
|
Project 7 |
14 |
48 |
4 |
|
Project 8 |
10 |
36 |
3 |
|
Project 9 |
1.2 |
18 |
3 |
-
Jika kita tidak bisa melakukan sebagian kecil dari sebuah proyek tetapi harus melakukan salah satu atau tidak ada proyek, bagaimana kita bisa memaksimalkan NPV?
-
Misalkan jika Project 4 dilaksanakan, Project 5 harus dilaksanakan. Bagaimana kami dapat memaksimalkan NPV?
-
Perusahaan penerbitan mencoba menentukan 36 buku mana yang harus diterbitkan tahun ini. File Pressdata.xlsx memberikan informasi berikut tentang setiap buku:
-
Proyeksi pendapatan dan biaya pengembangan (dalam ribuan dolar)
-
Halaman di setiap buku
-
Apakah buku ditujukan untuk audiens pengembang perangkat lunak (ditunjukkan dengan 1 di kolom E)
Perusahaan penerbitan dapat menerbitkan buku yang berjumlah hingga 8500 halaman tahun ini dan harus menerbitkan setidaknya empat buku yang ditujukan untuk pengembang perangkat lunak. Bagaimana perusahaan dapat memaksimalkan labanya?
-
Artikel ini diadaptasi dari Analisis Data dan Pemodelan Bisnis Microsoft Office Excel 2007 oleh Wayne L. Winston.
Buku bergaya kelas ini dikembangkan dari serangkaian presentasi oleh Wayne Winston, seorang profesor statistik dan bisnis terkenal yang mengkhususkan diri dalam aplikasi kreatif dan praktis Excel.










