Si vous devez créer des analyses statistiques ou techniques complexes, vous pouvez gagner du temps en utilisant l’Utilitaire d’analyse. Vous fournissez les données et les paramètres nécessaires à chaque analyse et l’utilitaire utilise les fonctions macro appropriées pour calculer et afficher les résultats dans une table. En plus des tables de résultats, certains outils génèrent des graphiques.
Les fonctions d’analyse des données peuvent être utilisées sur une seule feuille de calcul à la fois. Lorsque vous analysez des données sur des feuilles de calcul groupées, les résultats apparaissent sur la première feuille de calcul et des tables vides avec mise en forme apparaissent dans les autres. Pour analyser les données dans les autres feuilles de calcul, relancez l’outil d’analyse pour chaque feuille de calcul.
L’Utilitaire d’analyse comprend les outils décrits dans les sections suivantes. Pour accéder à ces outils, cliquez sur Analyse des données dans le groupe Analyse dans l’onglet Données. Si la commande Analyse des données n’est pas disponible, téléchargez la macro complémentaire Utilitaire d’analyse.
-
Cliquez sur l’onglet Fichier, sur Options, puis sur la catégorie Macros complémentaires.
-
Dans la zone Gérer, sélectionnez Compléments Excel, puis cliquez sur OK.
Si vous utilisez Excel pour Mac, dans le menu Fichier, accédez à Outils > Compléments Excel.
-
Dans la boîte de dialogue Compléments, cochez la case Utilitaire d’analyse, puis cliquez sur OK.
-
Si l’Analysis ToolPak ne figure pas dans la zone Macros complémentaires disponibles, cliquez sur Parcourir pour le rechercher.
-
Si vous recevez un message indiquant qu’il n’est pas installé sur votre ordinateur, cliquez sur Oui pour l’installer.
-
Remarque : Pour inclure Visual Basic pour Applications (VBA) pour l’Utilitaire d’analyse, vous pouvez charger le complément Analysis ToolPak - VBA en procédant de la même façon que pour télécharger l’Utilitaire d’analyse. Dans la zone disponible Compléments, cochez la case Analysis ToolPak - VBA.
Les outils d’analyse Anova permettent d’effectuer différents types d’analyse de la variance. L’outil à utiliser dépend du nombre de facteurs et du nombre d’échantillons extraits des populations à tester.
Anova : un facteur
Cet outil effectue une analyse simple de la variance des données pour deux échantillons ou plus. L’analyse fournit un test de l’hypothèse selon laquelle chaque échantillon est tiré de la même distribution de probabilité sous-jacente par rapport à l’hypothèse alternative selon laquelle les distributions de probabilité sous-jacentes ne sont pas les mêmes pour tous les échantillons. S’il n’existe que deux exemples, vous pouvez utiliser la fonction de feuille de calcul T.TEST. Avec plus de deux échantillons, il n’y a pas de généralisation pratique de T.TEST et le modèle Single Factor Anova peuvent être appelés à la place.
Anova : deux facteurs avec réplication
Cet outil d’analyse convient lorsqu’il est possible de classer les données en fonction de deux dimensions différentes. Imaginons une étude sur la hauteur des plantes auxquelles on associe différentes marques d’engrais (par exemple, A, B, C) et qui sont conservés à des températures différentes (par exemple, basse, élevée). Pour chaque paire possible {engrais, température}, on obtient un nombre égal d’observations pour la hauteur des plantes. Avec cet outil Anova, il est possible de tester les hypothèses suivantes :
-
Les plantes dont la hauteur est mesurée pour des marques d’engrais différentes proviennent de la même population sous-jacente. Il n’est pas tenu compte des températures dans cette analyse.
-
Les plantes dont la hauteur est mesurée avec des niveaux de température différents proviennent de la même population sous-jacente. Il n’est pas tenu compte des marques d’engrais dans cette analyse.
Prise en compte de l’incidence des différences entre les marques d’engrais notées au premier point et des différences de température notées au second point, les six échantillons représentant toutes les paires de valeurs {engrais, température} proviennent de la même population. L’hypothèse alternative consiste à supposer qu’il existe des effets liés aux paires spécifiques {engrais, température} au-delà des différences, qui sont liés à l’engrais uniquement ou à la température uniquement.
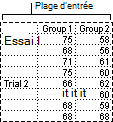
Anova : deux facteurs sans réplication
Cet outil d’analyse est utile lorsque les données sont classées en fonction de deux dimensions différentes comme dans le cas du test à deux facteurs avec réplication. Toutefois, l’utilisation de cet outil suppose une seule observation pour chaque paire (par exemple, chaque paire {engrais, température} de l’exemple précédent).
Les fonctions de feuille de calcul CORREL et PEARSON calculent le coefficient de corrélation entre deux variables de mesure lorsque des mesures sur chaque variable sont observées pour chacun des N sujets. (Toute observation manquante pour un sujet entraîne l’ignorer dans l’analyse.) L’outil d’analyse de corrélation est particulièrement utile lorsqu’il existe plus de deux variables de mesure pour chacun des N sujets. Il fournit une table de sortie, une matrice de corrélation, qui montre la valeur de CORREL (ou PEARSON) appliquée à chaque paire possible de variables de mesure.
Le coefficient de corrélation, comme la covariance, est une mesure de la mesure dans laquelle deux variables de mesure « varient ensemble ». Contrairement à la covariance, le coefficient de corrélation est mis à l’échelle de sorte que sa valeur soit indépendante des unités dans lesquelles les deux variables de mesure sont exprimées. (Par exemple, si les deux variables de mesure sont le poids et la hauteur, la valeur du coefficient de corrélation est inchangée si le poids est converti de livres en kilogrammes.) La valeur de tout coefficient de corrélation doit être comprise entre -1 et +1 inclus.
Vous pouvez utiliser l’outil d’analyse de corrélation pour étudier chaque paire de variables numériques et déterminer si elles corrèlent, c’est-à-dire si les valeurs élevées d’une variable ont tendance à suivre les valeurs élevées de l’autre variable (on parle de corrélation positive), si les valeurs faibles d’une variable ont tendance à suivre les valeurs élevées de l’autre variable (on parle de corrélation négative) ou bien enfin, si les valeurs des deux variables ne sont pas liées (corrélation proche de 0 (zéro)).
Les outils de calcul de la corrélation et de la covariance peuvent tous deux être utilisés dans le même contexte, c’est-à-dire lorsque N variables numériques différentes font l’objet d’une observation sur un groupe d’individus. Ces deux outils permettent tous deux d’obtenir une table de résultats, une matrice, qui montre respectivement le coefficient de corrélation ou la covariance entre chaque paire de variables numériques. La différence entre les deux outils est liée au fait que les coefficients de corrélation sont échelonnés de façon à être compris entre -1 et +1 inclus. Les covariances ne sont pas échelonnées. Le coefficient de corrélation et la covariance montrent dans quelle mesure deux variables « varient ensemble ».
L’outil Covariance calcule la valeur de la fonction de feuille de calcul COVARIANCE. P pour chaque paire de variables de mesure. (Utilisation directe de COVARIANCE. P plutôt que l’outil de covariance est une alternative raisonnable lorsqu’il n’y a que deux variables de mesure, c’est-à-dire N=2.) L’entrée sur la diagonale de la table de sortie de l’outil Covariance dans la ligne i, colonne i est la covariance de la i-ième variable de mesure avec elle-même. Il s’agit simplement de la variance de population pour cette variable, telle que calculée par la fonction de feuille de calcul VAR.P.
Vous pouvez utiliser l’outil d’analyse de covariance pour étudier chaque paire de variables numériques et déterminer si elles corrèlent, c’est-à-dire si les valeurs élevées d’une variable ont tendance à suivre les valeurs élevées de l’autre variable (on parle de corrélation positive), si les valeurs faibles d’une variable ont tendance à suivre les valeurs élevées de l’autre variable (on parle de corrélation négative) ou bien enfin, si les valeurs des deux variables ne sont pas liées (corrélation proche de 0 (zéro)).
L’outil d’analyse des statistiques génère un rapport statistique univariable à partir des données de la plage d’entrée et fournit des informations sur la tendance centrale et la variabilité des données.
L’outil d’analyse du lissage exponentiel prédit une valeur basée sur la prévision de la période précédente, ajustée pour l’erreur de cette prévision précédente. L’outil utilise la constante de lissage a, dont l’ampleur détermine le degré de réponse des prévisions aux erreurs de la prévision précédente.
Remarque : Les constantes de lissage prennent généralement les valeurs 0,2 à 0,3. Ces valeurs indiquent que la prévision doit être ajustée à 20 ou 30 pour cent pour l’erreur de prévision précédente. Des valeurs de constantes plus élevées entraînent des réponses plus rapides, mais risquent de générer des projections inconstantes. Des valeurs de constantes moins élevées peuvent entraîner des décalages importants pour les valeurs de prévision.
L’outil d’analyse Test F de la variance pour deux échantillons permet d’effectuer le test F sur deux échantillons afin de comparer les variances de deux populations.
Par exemple, vous pouvez appliquer le test F sur les échantillons de scores établis dans une compétition de natation par deux équipes. Cet outil permet de tester l’hypothèse nulle selon laquelle ces deux échantillons proviennent de distributions avec des variances égales et l’hypothèse alternative selon laquelle les variances ne sont pas égales dans les distributions sous-jacentes.
Cet outil calcule la valeur f pour un test statistique F (ou un pourcentage). Si la valeur de f est proche de 1 alors on peut en déduire que les variances des populations sous-jacentes sont égales. Dans la table, f < 1 « P(F <= f) unilatéral » donne la probabilité d’observation d’une valeur du test statistique F inférieure à f lorsque les variances des populations sont égales et « F Critique unilatéral » donne une valeur critique inférieure à 1 pour le seuil Alpha significatif choisi. f > 1, « P(F <= f) unilatéral » donne la probabilité d’observation d’une valeur du test statistique F supérieure à f lorsque les variances des populations sont égales, et « F Critique unilatéral » donne une valeur critique supérieure à 1 pour le seuil Alpha.
L’outil d’analyse de Fourier permet de résoudre des problèmes dans les systèmes linéaires et analyse les données en utilisant la « transformée de Fourier rapide » pour transformer des données. Cet outil permet également les transformations inverses, dans lesquelles l’inverse des données transformées renvoie les données d’origine.
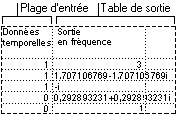
L’outil d’analyse Histogramme calcule les fréquences individuelles et cumulatives pour une plage de cellules de données et des emplacements de données. Cet outil génère des données pour un certain nombre d’occurrences d’une valeur dans une série de données.
Par exemple, dans une classe de 20 étudiants, vous pouvez déterminer la distribution des notes sous forme de notation alphabétique. Un histogramme présente les bornes et le nombre de notes entre la borne inférieure et la borne actuelle. Le score unique le plus fréquent représente le mode des données.
Conseil : Dans Excel 2016, vous pouvez désormais créer un histogramme ou un graphique de Pareto.
L’outil de calcul de la moyenne mobile permet de projeter des valeurs sur une période prévisionnelle en se basant sur la valeur moyenne de la variable sur un nombre spécifique de périodes précédentes. Une moyenne mobile fournit des informations de tendance que la moyenne simple des données historiques masque. Utilisez cet outil pour établir des prévisions de ventes, de gestion de stock par exemple. Chaque valeur prévisionnelle est basée sur la formule suivante.
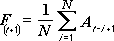
où :
-
N est le nombre de périodes antérieures à inclure dans la moyenne mobile
-
A j est la valeur actuelle au moment j
-
F j est la valeur prévisionnelle au moment j
L’outil d’analyse Générateur de nombre aléatoire complète une série avec des nombres aléatoires indépendants qui proviennent d’une distribution. Vous pouvez caractériser les sujets d’une population avec une distribution des probabilités. Par exemple, vous pouvez utiliser une loi normale de distribution pour caractériser la population des tailles d’individus ou bien utiliser la distribution de Bernoulli de deux résultats possibles pour caractériser la population des résultats des tirages à pile ou face.
L’outil d’analyse Rank and Percentile génère une table qui contient le rang ordinal et le pourcentage de chaque valeur dans un jeu de données. Vous pouvez analyser la position relative des valeurs dans un jeu de données. Cet outil utilise les fonctions de feuille de calcul RANK. EQ etPERCENTRANK. INC. Si vous souhaitez tenir compte des valeurs liées, utilisez rank . La fonction EQ , qui traite les valeurs liées comme ayant le même rang, ou utilise la fonction RANK.Fonction AVG , qui retourne le classement moyen pour les valeurs liées.
L’outil Régression permet d’effectuer une analyse de régression linéaire en utilisant la méthode des moindres carrés afin de rechercher une droite à partir des valeurs observées. Vous pouvez analyser la façon dont une variable dépendante simple est affectée par les valeurs d’une ou de plusieurs variables indépendantes. Par exemple, vous pouvez analyser la façon dont les performances d’un athlète sont influencées par des facteurs tels que l’âge, la taille et le poids. Vous pouvez répartir les parts que chacun de ces trois facteurs représente dans les performances en vous basant sur une série de données de performances, puis utiliser les résultats pour prédire les performances d’un nouvel athlète qui n’a encore fait l’objet d’aucun test.
L’outil Régression utilise la fonction de feuille de calcul LINEST.
L’outil d’analyse Échantillonnage crée un échantillon à partir d’une population en traitant comme une population la série de données entrée. Si la population est trop importante pour être traitée ou représentée sous forme de graphique, vous pouvez utiliser un échantillon représentatif. Vous pouvez également créer un échantillon qui contient uniquement les valeurs d’un cycle particulier si vous pensez que les données sont périodiques. Par exemple, si la série de données contient des chiffres de ventes trimestrielles, le fait de créer un échantillon à partir d’une périodicité égale à quatre place les valeurs du même trimestre dans la série résultante.
Les outils d’analyse Test t de comparaison de deux échantillons permettent de tester l’égalité des moyennes de population qu’il est possible de déduire sur la base de chaque échantillon. Trois outils pour trois assomptions différentes : les variances de la population sont égales, les variances de la population ne sont pas égales, les données des deux échantillons sont des données observées avant traitement et après traitement sur les mêmes sujets.
Pour les trois outils ci-dessous, une valeur statistique t est calculée et figure dans les tables de résultats (« t Stat »). En fonction des données, cette valeur, t, peut être négative ou non négative. Sur la base de l’assomption de l’égalité des moyennes de population sous-jacentes, t < 0, « P(T <= t) unilatéral » donne la probabilité que la valeur statistique t observée est plus négative que la valeur t de la table. t >=0, « P(T <= t) unilatéral » donne la probabilité que la valeur statistique t observée est plus positive que la valeur t de la table. La valeur t critique du test unilatéral donne la valeur du seuil, de sorte que la probabilité d’observer une valeur statistique t supérieure ou égale à la valeur critique t du test unilatéral est Alpha.
« P(T <= t) bilatéral » donne la probabilité que la valeur statistique t observée est supérieure en valeur absolue à la valeur t de la table. La valeur critique P du test bilatéral donne la valeur du seuil, de sorte que la probabilité d’une valeur statistique t observée supérieure en valeur absolue à la valeur critique P du test bilatéral est Alpha.
Test t pour le calcul des moyennes de deux échantillons appariés
Vous pouvez utiliser le test t apparié lorsque les observations sur les échantillons sont naturellement appariées, par exemple, lorsqu’un groupe est testé deux fois : avant et après une expérimentation. Cet outil d’analyse et sa formule permettent d’effectuer un test t de Student pour deux échantillons appariés afin de déterminer si les observations relevées avant et après traitement proviennent de distributions avec des moyennes égales de population. Ce test ne suppose pas que les variances des deux populations sont égales.
Remarque : Parmi les résultats générés par cet outil figure la variance cumulée, une mesure cumulée de la répartition des données sur la moyenne, qui est dérivée de la formule suivante.
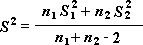
Test t pour deux échantillons avec pour assomption l’égalité des variances
Cet outil d’analyse permet d’effectuer un test t de Student pour deux échantillons. Pour ce test, l’assomption est que les deux séries de données proviennent de distributions avec les mêmes variances. On parle de test t homoscédastique. Vous pouvez utiliser ce test t de Student pour déterminer si les deux échantillons proviennent de distributions avec des moyennes égales de population.
Test t pour deux échantillons avec pour assomption l’inégalité des variances
Cet outil d’analyse permet d’effectuer un test t de Student pour deux échantillons. Pour ce test, l’assomption est que les deux séries de données proviennent de distributions avec des variances inégales. On parle de test t hétéroscédastique. Tout comme dans le cas précédent de l’égalité des variances, vous pouvez utiliser ce test t pour déterminer si les deux échantillons proviennent de distributions avec des moyennes égales de population. Utilisez ce test si les sujets des deux échantillons sont différents. Utilisez le test pour échantillon apparié, décrit dans l’exemple qui suit, pour un groupe de sujets identiques et si les mesures relevées pour les deux échantillons le sont avant et après traitement pour chaque sujet.
La formule suivante permet de calculer la valeur statistique t.
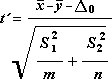
La formule suivante est utilisée pour calculer les degrés de liberté, df. Étant donné que le résultat du calcul n’est généralement pas un entier, la valeur de df est arrondie à l’entier le plus proche pour obtenir une valeur critique à partir de la table t. Fonction T de feuille de calcul Excel.TEST utilise la valeur df calculée sans arrondi, car il est possible de calculer une valeur pour T.TEST avec un df noninteger. En raison de ces différentes approches pour déterminer les degrés de liberté, les résultats de T.TEST et cet outil t-Test diffèrent dans le cas des variances inégales.
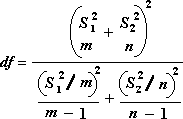
L’outil d’analyse z-Test : Two Sample for Moyennes effectue un test z à deux exemples pour les moyennes avec des variances connues. Cet outil est utilisé pour tester l’hypothèse null selon laquelle il n’existe aucune différence entre deux moyennes de population par rapport à des hypothèses alternatives unilatées ou bidirectiées. Si les variances ne sont pas connues, la fonction de feuille de calcul Z.TEST doit être utilisé à la place.
Lorsque vous utilisez le test z, assurez-vous de bien interpréter le résultat. « P(Z <= z) unilatéral » correspond à P(Z >= ABS(z)), la probabilité d’une valeur z au-delà de 0 dans le même sens que la valeur z observée lorsqu’il n’existe pas de différence entre les moyennes des populations. « P(Z <= z) bilatéral » correspond à P(Z >= ABS(z) ou Z <= -ABS(z)), la probabilité d’une valeur z au-delà de 0 dans les deux sens par rapport à la valeur z observée lorsqu’il n’existe aucune différence entre les moyennes de population. Le résultat bilatéral correspond simplement au résultat unilatéral multiplié par 2. Le test z peut également servir lorsque l’hypothèse nulle est la suivante : il existe une valeur spécifique différente de zéro pour la différence entre les deux moyennes de population. Par exemple, vous pouvez utiliser ce test pour déterminer les différences entre les performances de deux modèles de voitures.
Vous avez besoin d’une aide supplémentaire ?
Vous pouvez toujours poser des questions à un expert de la Communauté technique Excel ou obtenir une assistance dans la Communauté de support.
Voir aussi
Créer un histogramme dans Excel 2016
Créer un graphique Pareto dans Excel 2016
Charger l’utilitaire d’analyse dans Excel
Fonctions ENGINEERING (référence)
Vue d’ensemble des formules dans Excel
Comment éviter les formules incorrectes
Rechercher et corriger les erreurs dans les formules
Raccourcis clavier et les touches de fonction Excel










