Renvoie la probabilité d’une variable aléatoire suivant une loi Weibull. Utilisez cette distribution dans une analyse de fiabilité telle que le calcul du temps moyen de fonctionnement sans panne d’un appareil.
Syntaxe
LOI.WEIBULL(x;alpha;bêta;cumulative)
x représente la variable avec laquelle la fonction doit être calculée.
alpha représente un paramètre de la distribution.
bêta représente un paramètre de la distribution.
cumulative détermine la forme de la fonction.
Notes
-
Si les arguments x, alpha ou bêta ne sont pas numériques, la fonction LOI.WEIBULL renvoie la valeur d’erreur #VALEUR!.
-
Si x < 0, la fonction LOI.WEIBULL renvoie la valeur d’erreur #NOMBRE!.
-
Si alpha ≤ 0 ou si bêta ≤ 0, la fonction LOI.WEIBULL renvoie la valeur d’erreur #NOMBRE!.
-
L’équation pour la fonction de distribution cumulée de la loi Weibull est la suivante :
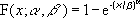
-
L’équation pour la fonction de densité de probabilité de la loi Weibull est la suivante :
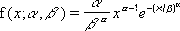
-
Lorsque alpha = 1, LOI.WEIBULL renvoie la distribution exponentielle avec :
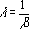
Exemples
|
x |
alpha |
bêta |
Formule |
Description (résultat) |
|
105 |
20 |
100 |
=LOI.WEIBULL([x];[alpha];[bêta];VRAI) |
Fonction de distribution cumulée selon la loi de Weibull pour les arguments spécifiés (0,929581) |
|
105 |
20 |
100 |
=LOI.WEIBULL([x];[alpha];[bêta];FAUX) |
Fonction de densité de probabilité de la loi Weibull pour les arguments spécifiés (0,035589) |










