Huomautus: Microsoft haluaa tarjota sinulle ajantasaisinta ohjesisältöä mahdollisimman nopeasti omalla kielelläsi. Tämä sivu on käännetty automaation avulla, ja siinä saattaa olla kielioppivirheitä tai epätarkkuuksia. Tarkoitus on, että sisällöstä on sinulle hyötyä. Kertoisitko sivun alareunassa olevan toiminnon avulla, oliko tiedoista hyötyä? Tästä pääset helposti artikkelin englanninkieliseen versioon .
Palauttaa hajontojen itseisarvojen keskiarvon. KESKIPOIKKEAMA on yksi tapa mitata aineistossa esiintyvää vaihtelua.
Syntaksi
KESKIPOIKKEAMA(luku1;luku2; ...)
Luku1; luku2; ... ovat 1–30 argumenttia, joiden poikkeamien itseisarvojen keskiarvon haluat laskea.
Huomautuksia
-
Argumenttien on oltava lukuja tai lukuja sisältäviä sarakeviittauksia.
-
Jos sarakeviittaus sisältää tekstiä tai totuusarvoja tai on tyhjä, arvot ohitetaan tai funktio palauttaa #ARVO!-virhearvon. Arvo nolla käsitellään normaalisti.
-
Keskipoikkeama lasketaan seuraavalla kaavalla:
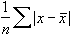
Syöteaineiston mittayksiköt vaikuttavat KESKIPOIKKEAMA-funktioon.
Esimerkki
|
Sar1 |
Sarake2: |
Sarake3: |
Sarake4: |
Sarake5: |
Sarake6: |
Sarake7: |
Kaava |
Kuvaus (tulos): |
|
4 |
5 |
6 |
7 |
5 |
4 |
3 |
=KESKIPOIKKEAMA[Sarake1],[Sarake2],[Sarake3],[Sarake4],[Sarake5][Sarake6][Sarake7]) |
Palauttaa lukujen poikkeaman itseisarvojen keskiarvon. (1,020408) |










