En este artículo se describen la sintaxis de la fórmula y el uso de la función ESTIMACION.LINEAL en Microsoft Excel. Encontrará vínculos con más información sobre cómo crear gráficos y realizar un análisis de regresión en la sección Vea también.
Descripción
La función ESTIMACION.LINEAL calcula las estadísticas de una línea con el método de los "mínimos cuadrados" para calcular la línea recta que mejor se ajuste a los datos y después devuelve una matriz que describe la línea. También puede combinar ESTIMACION.LINEAL con otras funciones para calcular las estadísticas de otros tipos de modelos que son lineales en los parámetros desconocidos, incluidas series polinómicas, logarítmicas, exponenciales y de potencias. Debido a que esta función devuelve una matriz de valores, debe ser especificada como fórmula de matriz. Encontrará las instrucciones correspondientes tras los ejemplos de este artículo.
La ecuación para la línea es la siguiente:
y = mx + b
- O bien -
y = m1x1 + m2x2 + ... + b
si hay varios rangos de valores x, donde los valores y dependientes son función de los valores x independientes. Los valores m son coeficientes que corresponden a cada valor x, y b es un valor constante. Observe que y, x y m pueden ser vectores. La matriz que devuelve la función ESTIMACION.LINEAL es {mn,mn-1,...,m1,b}. ESTIMACION.LINEAL también puede devolver estadísticas de regresión adicionales.
Sintaxis
ESTIMACION.LINEAL(conocido_y, [conocido_x], [constante], [estadística])
La sintaxis de la función ESTIMACION.LINEAL tiene los siguientes argumentos:
Sintaxis
-
Conocido_y Obligatorio. Es el conjunto de valores y que se conocen en la relación y = mx+b.
-
Si el rango de conocido_y ocupa una sola columna, cada columna de conocido_x se interpreta como una variable independiente.
-
Si el rango de conocido_y ocupa una sola fila, cada fila de conocido_x se interpreta como una variable independiente.
-
-
Conocido_x Opcional. Es un conjunto de valores x que pueden conocerse en la relación y = mx+b.
-
El rango de conocido_x puede incluir uno o varios conjuntos de variables. Si usa una sola variable, conocido_y y conocido_x pueden ser rangos con cualquier forma, siempre y cuando sus dimensiones sean iguales. Si usa más de una variable, conocido_y tiene que ser un vector (es decir, un rango compuesto por una fila o por una columna).
-
Si omite conocido_x, se supone que es la matriz {1,2,3,...} que tiene el mismo tamaño que conocido_y.
-
-
Constante Opcional. Es un valor lógico que especifica si se fuerza la constante b para que sea igual a 0.
-
Si omite el argumento constante o es VERDADERO, b se calcula normalmente.
-
Si constante es FALSO, b se establece como igual a 0 y los valores m se ajustan para adaptarse a y = mx.
-
-
Estadística Opcional. Es un valor lógico que especifica si se deben devolver estadísticas de regresión adicionales.
-
Si estadística es VERDADERO, ESTIMACION.LINEAL devuelve las estadísticas de regresión adicionales; como resultado, la matriz devuelta es {mn,mn-1,...,m1,b; sen,sen-1,...,se1,seb; r2,sey; F, df; ssreg,ssresid}.
-
Si omite estadística o es FALSO, ESTIMACION.LINEAL solo devuelve los coeficientes m y la constante b.
Las estadísticas de regresión adicional son las siguientes.
-
|
Estadística |
Descripción |
|---|---|
|
se1,se2,...,sen |
Los valores de error estándar para los coeficientes m1,m2,...,mn. |
|
seb |
El valor de error estándar para la constante b (seb = #N/A cuando constante es FALSO). |
|
r2 |
El coeficiente de determinación. Compara los valores y calculados y reales, y los rangos con valor de 0 a 1. Si es 1, hay una correlación perfecta en la muestra, es decir, no hay diferencia entre el valor y calculado y el valor y real. En el otro extremo, si el coeficiente de determinación es 0, la ecuación de regresión no es útil para predecir un valor y. Para obtener información sobre cómo se calcula2 , vea la sección "Observaciones" más adelante en este tema. |
|
sey |
El error estándar para el cálculo y. |
|
F |
La estadística F o valor F observado. Use la estadística F para determinar si la relación observada entre las variables dependientes e independientes se produce por azar. |
|
df |
Grados de libertad. Use los grados de libertad para encontrar valores F críticos en una tabla estadística. Compare los valores que encuentre en la tabla con la estadística F devuelta por ESTIMACION.LINEAL para determinar un nivel de confianza para el modelo. Para obtener información sobre el cálculo de df, vea la sección "Observaciones" más adelante en este tema. El ejemplo 4 muestra el uso de F y df. |
|
ssreg |
La suma de regresión de los cuadrados. |
|
ssresid |
La suma residual de los cuadrados. Para obtener información sobre el cálculo de ssreg y ssresid, vea la sección "Observaciones" más adelante en este tema. |
La ilustración siguiente muestra el orden en que se devuelven las estadísticas de regresión adicionales.

Observaciones
-
Puede describir cualquier línea recta con la pendiente y la intersección y:
Pendiente (m):
Para encontrar la pendiente de una línea, a menudo escrita como m, tome dos puntos en la línea, (x1,y1) y (x2,y2); la pendiente es igual a (y2 - y1)/(x2 - x1).Intersección Y (b):
La intersección y de una línea, a menudo escrita como b, es el valor de y en el punto donde la línea cruza el eje y.La ecuación de una línea recta es y = mx + b. Si conoce los valores de m y b, puede calcular cualquier punto de la línea insertando el valor y o x en esa ecuación. También puede usar la función TENDENCIA.
-
Si solo tiene una variable x independiente, puede obtener los valores de la pendiente y de la intersección y directamente con las fórmulas siguientes:
Pendiente:
=INDICE(ESTIMACION.LINEST(known_y;known_x);1)Intersección Y:
=INDICE(ESTIMACION.LINEST(known_y;known_x);2) -
La exactitud de la línea calculada por la función ESTIMACION.LINEAL depende del grado de dispersión de los datos. Cuanto más lineales sean los datos, más exacto será el modelo de ESTIMACION.LINEAL. ESTIMACION.LINEAL usa el método de los mínimos cuadrados para determinar el mejor ajuste para los datos. Si solo tiene una variable x independiente, los cálculos para m y b se basan en las fórmulas siguientes:
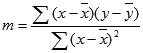
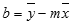
Donde x e y son medias de muestra; es decir, x = PROMEDIO(conocido x) e y = PROMEDIO(known_y).
-
Las funciones de ajuste de línea y curva ESTIMACION.LINEAL y ESTIMACION.LOGARI PUEDEN calcular la mejor línea recta o curva exponencial que se ajuste a sus datos. Sin embargo, tiene que decidir cuál de los dos resultados se ajusta mejor a sus datos. Puede calcular TENDENCIA(known_y,known_x) para una línea recta o CRECIMIENTO(known_y, known_x) para una curva exponencial. Estas funciones, sin el argumento de la new_x , devuelven una matriz de valores y pronosticados a lo largo de esa línea o curva en los puntos de datos reales. Después, puede comparar los valores pronosticados con los valores reales. Es posible que desee representarlos en un gráfico para realizar una comparación visual.
-
En el análisis de regresión, Excel calcula para cada punto la diferencia al cuadrado entre el valor y calculado para ese punto y su valor y real. La suma de estas diferencias al cuadrado se denomina suma de los cuadrados residual, ssresid. Excel calcula a continuación la suma total de los cuadrados, sstotal. Si omite el argumento constante o es VERDADERO, la suma total de los cuadrados es la suma de las diferencias al cuadrado entre los valores y reales y la media de los mismos. Cuando el argumento constante = FALSO, la suma total de los cuadrados es la suma de los cuadrados de los valores y reales (sin restar el valor y medio de cada valor y individual). Puede hallar la suma de regresión de los cuadrados, ssreg, a partir de ssreg = sstotal - ssresid. Cuanto menor sea la suma residual de los cuadrados, en comparación con la suma total de los cuadrados, mayor será el valor del coeficiente de determinación, r2, que es un indicador de lo bien que la ecuación resultante del análisis de regresión explica la relación entre las variables. El valor de r2 es igual a ssreg/sstotal.
-
En algunos casos, una o varias de las columnas x (supongamos que y y x están en columnas) pueden no tener valor predictivo adicional en presencia de las otras columnas x. En otras palabras, eliminar una o varias columnas x puede producir valores y pronosticados que son igualmente exactos. En ese caso, estas columnas x redundantes deberían omitirse del modelo de regresión. Este fenómeno se denomina “colinealidad” porque cualquier columna x redundante se puede expresar como una suma de múltiplos de las columnas x no redundantes. ESTIMACION.LINEAL comprueba la colinealidad y quita cualquier columna x redundante del modelo de regresión cuando las identifica. Puede reconocer las columnas x eliminadas en el resultado de ESTIMACION.LINEAL como aquellas con coeficientes 0 así como con valores de 0. Si quita una o varias columnas por redundantes, entonces df se ve afectado porque df depende del número de columnas x usadas con fines predictivos. Para más información sobre el cálculo de df, vea el ejemplo 4. Si modifica df modifica porque ha quitado las columnas x redundantes, los valores de sey y F también se verán afectados. La colinealidad debería ser relativamente insólita en la práctica. No obstante, un caso en el que es más probable que se produzca es cuando algunas columnas x contienen solo valores 0 y 1 como indicadores de si un sujeto de un experimento pertenece o no a un grupo en concreto. Si omite constante o es VERDADERO, ESTIMACION.LINEAL inserta una columna x adicional de todo unos (1) para dar forma a la intersección. Si tiene una columna con un 1 para cada sujeto que sea varón, o 0 si no lo es, y tiene también una columna con un 1 para cada sujeto que sea mujer, o 0 si no lo es, esta última columna es redundante porque puede obtener las entradas de la misma de restar la entrada de la columna "indicador de varón" de la entrada de la columna adicional de todo unos (1) agregada por ESTIMACION.LINEAL.
-
Calcule el valor de df como sigue, no se quite ninguna columna x del modelo debido a la colinealidad: si hay k columnas de conocido_x y omite constante o es VERDADERO, entonces df = n – k – 1. Si constante = FALSO, entonces df = n - k. En ambos casos, cada columna x quitada debido a la colinealidad aumenta df en 1.
-
Cuando especifique como argumento una constante de matriz (como conocido_x), use comas para separar los valores contenidos en una misma fila y puntos y comas para separar las filas. Los caracteres separadores pueden ser diferentes según la configuración regional.
-
Observe que los valores y pronosticados por la ecuación de regresión pueden no ser válidos si quedan fuera del rango de los valores y empleados para determinar la ecuación.
-
El algoritmo subyacente usado en la función ESTIMACION.LINEAL es diferente del algoritmo subyacente usado en las funciones PENDIENTE e INTERSECCION.EJE. La diferencia entre estos algoritmos puede producir resultados distintos cuando los datos son indeterminados y colineales. Por ejemplo, si los puntos de datos del argumento conocido_y son 0 y los puntos de datos del argumento conocido_x son 1:
-
ESTIMACION.LINEAL devuelve un valor 0. El algoritmo de la función ESTIMACION.LINEAL está diseñado para devolver resultados razonables para los datos colineales y, en este caso, se puede encontrar al menos una respuesta.
-
PENDIENTE e INTERSECCION.EJE devuelven un #DIV/0! #VALOR!. El algoritmo de las funciones PENDIENTE e INTERSECCION.EJE está diseñado para buscar solo una respuesta y, en este caso, puede haber más de una respuesta.
-
-
Además de usar ESTIMACION.LOGARITMICA para calcular estadísticas para otros tipos de regresión, puede usar ESTIMACION.LINEAL para calcular un rango de tipos de regresión diferentes escribiendo funciones de las variables x e y como series x e y para ESTIMACION.LINEAL. Por ejemplo, la fórmula siguiente:
=ESTIMACION.LINEAL(valores y, valores x^COLUMNA($A:$C))
funciona si se dispone de una única columna de valores y y una única columna de valores x para calcular la aproximación cúbica (polinómica de orden 3) de esta forma:
y = m1*x + m2*x^2 + m3*x^3 + b
Puede ajustar esta fórmula para calcular otros tipos de regresión, pero en algunos casos, es necesario ajustar los valores de salida y otras estadísticas.
-
El valor de la prueba F que devuelve la función ESTIMACION.LINEAL y el que devuelve la función PRUEBA.F son diferentes. ESTIMACION.LINEAL devuelve la estadística F, mientras que PRUEBA.F devuelve la probabilidad.
Ejemplos
Ejemplo 1: Pendiente e intersección con eje y
Copie los datos del ejemplo en la siguiente tabla y péguelos en la celda A1 de una nueva hoja de cálculo de Excel. Para que las fórmulas muestren los resultados, selecciónelas, presione F2 y luego ENTRAR. Si lo necesita, puede ajustar el ancho de las columnas para ver todos los datos.
|
Y conocido |
X conocido |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Resultado (pendiente) |
Resultado (intersección y) |
|
2 |
1 |
|
Fórmula (fórmula de matriz en celdas A7:B7) |
|
|
=ESTIMACION.LINEAL(A2:A5;B2:B5;;FALSO) |
Ejemplo 2: Regresión lineal simple
Copie los datos del ejemplo en la siguiente tabla y péguelos en la celda A1 de una nueva hoja de cálculo de Excel. Para que las fórmulas muestren los resultados, selecciónelas, presione F2 y luego ENTRAR. Si lo necesita, puede ajustar el ancho de las columnas para ver todos los datos.
|
Mes |
Ventas |
|---|---|
|
1 |
$3.100 |
|
2 |
$4.500 |
|
3 |
$4.400 |
|
4 |
$5.400 |
|
5 |
$7.500 |
|
6 |
$8.100 |
|
Fórmula |
Resultado |
|
=SUMA(ESTIMACION.LINEAL(B1:B6, A1:A6)*{9,1}) |
11000 $ |
|
Calcula la estimación de las ventas en el noveno mes, basándose en las ventas de los meses 1 al 6. |
Ejemplo 3: Regresión lineal múltiple
Copie los datos del ejemplo en la siguiente tabla y péguelos en la celda A1 de una nueva hoja de cálculo de Excel. Para que las fórmulas muestren los resultados, selecciónelas, presione F2 y luego ENTRAR. Si lo necesita, puede ajustar los anchos de la columna para ver todos los datos.
|
Superficie (x1) |
Oficinas (x2) |
Entradas (x3) |
Antigüedad (x4) |
Valor tasado (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142000 $ |
|
2333 |
2 |
2 |
1,2 |
144000 $ |
|
2356 |
3 |
1,5 |
33 |
151000 $ |
|
2379 |
3 |
2 |
43 |
150000 $ |
|
2402 |
2 |
3 |
53 |
139000 $ |
|
2425 |
4 |
2 |
23 |
169 000 $ |
|
2448 |
2 |
1,5 |
99 |
126 000 $ |
|
2471 |
2 |
2 |
34 |
142 900 $ |
|
2494 |
3 |
3 |
23 |
163 000 $ |
|
2517 |
4 |
4 |
55 |
169 000 $ |
|
2540 |
2 |
3 |
22 |
149 000 $ |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Fórmula (fórmula de matriz dinámica especificada en A19) |
||||
|
=ESTIMACION.LINEAL(E2:E12;A2:D12;VERDADERO;VERDADERO) |
Ejemplo 4: Usar las estadísticas F y r2
En el ejemplo anterior, el coeficiente de determinación, o r2, es 0,99675 (vea la celda A17 en el resultado de ESTIMACION.DE.LÍNEA), que indicaría una relación estrecha entre las variables independientes y el precio de venta. Puede usar la estadística F para determinar si estos resultados, con este valor r2 tan alto, se produjeron por azar.
Suponga por un momento que en realidad no existe relación entre las variables, pero que ha extraído una muestra peculiar de 11 edificios de oficinas que hace que el análisis estadístico demuestre una relación marcada. El término "alfa" se usa para la probabilidad de llegar a la conclusión errónea de que existe una relación.
Los valores F y df del resultado de la función ESTIMACION.LINEAL se pueden usar para determinar la probabilidad de que se produzca por azar un valor F más elevado. F se puede comparar con los valores críticos de las tablas de distribución F publicadas o se puede usar la función DISTR.F de Excel para calcular la probabilidad de que se produzca por azar un valor F mayor. La distribución F apropiada tiene los grados de libertad v1 y v2. Si n es el número de puntos de datos y omite la constante o es VERDADERO, entonces v1 = n – df – 1 y v2 = df. Si la constante = FALSO, entonces v1 = n – df y v2 = df. La función DISTR.F ( con la sintaxis DISTR.F(F,v1,v2) ) devolverá la probabilidad de que se produzca por azar un valor F superior. En este ejemplo, df = 6 (celda B18) y F = 459,753674 (celda A18).
Suponiendo un valor alfa de 0,05, v1 = 11 – 6 – 1 = 4 y v2 = 6, el valor crítico de F es 4,53. Puesto que F = 459,753674 es mucho más elevado que 4,53, es extremadamente improbable que un valor F tan elevado se produzca por azar. (Con Alfa = 0,05, la hipótesis de que no hay relación entre conocido_y y conocido_x hay que rechazarla cuando F sobrepasa el nivel crítico, 4,53). Puede usar la función DISTR.F de Excel para obtener la probabilidad de que un valor F tan elevado se produzca por azar. Por ejemplo, DISTR.F(459,753674; 4; 6) = 1,37E-7, una probabilidad sumamente pequeña. Se puede concluir, bien buscando el nivel crítico de F en una tabla, bien con la función DISTR.F, que la ecuación de regresión es útil para predecir el valor tasado de los edificios de oficinas de esta área. Recuerde que es vital usar los valores correctos de v1 y v2 calculados en el párrafo anterior.
Ejemplo 5: Calcular la estadística t
Otra prueba hipotética determinará si cada coeficiente de la pendiente es útil para calcular el valor tasado de un edificio de oficinas del ejemplo 3. Por ejemplo, para probar si el coeficiente de antigüedad es significativo estadísticamente, divida -234,24 (coeficiente de la pendiente de antigüedad) por 13,268 (el error estándar calculado de los coeficientes de antigüedad en la celda A15). El siguiente es el valor t observado:
t = m4 ÷ se4 = -234,24 ÷ 13,268 = -17,7
Si el valor absoluto de t es suficientemente alto, puede deducirse que el coeficiente de la pendiente es útil para calcular el valor tasado del edificio de oficinas del ejemplo 3. La siguiente tabla muestra los valores absolutos de los 4 valores t observados.
Si consulta una tabla de un manual de estadística, observará que el valor t crítico, de dos colas, con 6 grados de libertad y alfa = 0,05 es 2,447. Este valor crítico puede encontrarse también con la función DISTR.T.INV de Excel. DISTR.T.INV(0,05,6) = 2,447. Puesto que el valor absoluto de t, 17,7, es superior a 2,447, la antigüedad es una variable importante para calcular el valor tasado de un edificio de oficinas. El significado estadístico de cada una de las demás variables independientes puede probarse de forma similar. Los siguientes son los valores t observados para cada una de las variables independientes.
|
Variable |
valor t observado |
|---|---|
|
Superficie |
5,1 |
|
Número de oficinas |
31,3 |
|
Número de entradas |
4,8 |
|
Edad |
17,7 |
Todos estos valores tienen un valor absoluto superior a 2,447; por tanto, todas las variables usadas en la ecuación de regresión son útiles para predecir el valor tasado de los edificios de oficinas de esta área.







