In diesem Artikel werden die Formelsyntax und die Verwendung der Funktion RGP in Microsoft Excel beschrieben. Verknüpfungen zu weiteren Informationen über das Erstellen von Diagrammen und Ausführen einer Regressionsanalyse finden Sie im Abschnitt Siehe auch.
Beschreibung
Die Funktion RGP berechnet die Statistik für eine Linie nach der Methode der kleinsten Quadrate, um eine gerade Linie zu berechnen, die am besten an die Daten angepasst ist, und gibt dann eine Matrix zurück, die die Linie beschreibt. Sie können RGP auch mit anderen Funktionen kombinieren, um die Statistiken für andere Modelltypen zu berechnen, die lineare unbekannte Parameter aufweisen, einschließlich polynomischer, logarithmischer und exponentieller Reihen sowie Potenzen. Da diese Funktion eine Matrix von Werten zurückgibt, muss die Formel als Matrixformel eingegeben werden. Anweisungen dazu sind nach den Beispielen in diesem Artikel angegeben.
Die Gleichung einer solchen Geraden lautet:
y = mx + b
– oder –
y = m1x1 + m2x2 + ... + b
, wenn mehrere Bereiche von x-Werten vorhanden sind, wobei die abhängigen y-Werte eine Funktion der unabhängigen x-Werte sind. Die m-Werte sind Koeffizienten, die jedem x-Wert entsprechen, und b ist ein konstanter Wert. Beachten Sie, dass y, x und m Vektoren sein können. Das Array, das die LINEST-Funktion zurückgibt, ist {mn,mn-1,...,m1,b}. LINEST kann auch zusätzliche Regressionsstatistiken zurückgeben.
Syntax
RGP(Y_Werte;[X_Werte];[Konstante];[Stats])
Die Syntax der Funktion RGP weist die folgenden Argumente auf:
Syntax
-
Y_Werte Erforderlich. Die y-Werte, die Ihnen bereits aus der Beziehung y = mx + b bekannt sind.
-
Besteht der Bereich der Y_Werte aus nur einer Spalte, wird jede Spalte für X_Werte als eigenständige Variable interpretiert.
-
Besteht der Bereich der Y_Werte aus nur einer Zeile, wird jede Zeile für X_Werte als eigenständige Variable interpretiert.
-
-
X_Werte Optional. Die x-Werte, die Ihnen möglicherweise bereits aus der Beziehung y = mx + b bekannt sind.
-
Der Bereich der X_Werte kann eine oder mehrere Variablengruppen umfassen. Wird nur eine Variable verwendet, können Y_Werte und X_Werte Bereiche beliebiger Form sein, solange sie dieselben Dimensionen haben. Werden mehrere Variablen verwendet, muss Y_Werte ein Vektor sein (das heißt ein Bereich, der aus nur einer Zeile oder nur einer Spalte besteht).
-
Fehlt die Angabe X_Werte, wird an ihrer Stelle die Matrix {1.2.3...} angenommen, die genauso viele Elemente wie Y_Werte enthält.
-
-
Konstante Optional. Ein Wahrheitswert, der angibt, ob die Konstante b den Wert 0 annehmen soll.
-
Ist Konstante mit WAHR belegt oder nicht angegeben, wird b normal berechnet.
-
Ist Konstante mit FALSCH belegt, wird b gleich 0 festgelegt, und die m-Werte werden so angepasst, dass sie zu der Beziehung y = mx passen.
-
-
Stats Optional. Ein Wahrheitswert, der angibt, ob zusätzliche Regressionskenngrößen zurückgegeben werden sollen.
-
Wenn stats den Wert TRUE hat, gibt LINEST die zusätzlichen Regressionsstatistiken zurück. Daher ist das zurückgegebene Array {mn,mn-1,...,m1,b; sen,sen-1,...,se1,seb; r2,sey; F,df; ssreg,ssresid}.
-
Ist Stats mit FALSCH belegt oder nicht angegeben, gibt RGP nur die m-Koeffizienten sowie die Konstante b zurück.
Die folgenden Regressionskenngrößen (-statistiken) können zusätzlich ermittelt werden:
-
|
Kenngröße (Statistik) |
Beschreibung |
|---|---|
|
se1;se2;...;sen |
Sind die Standardfehler der Koeffizienten m1;m2;...;mn. |
|
seb |
Der Standardfehler der Konstanten b (seb = #NV, wenn Konstante mit FALSCH belegt ist). |
|
r2 |
Das Bestimmtheitsmaß. Vergleicht die erwarteten mit den tatsächlichen y-Werten und kann Werte von 0 bis 1 annehmen. Besitzt es den Wert 1, besteht für die Stichprobe eine vollkommene Korrelation: ein erwarteter y-Wert und der entsprechende tatsächliche y-Wert unterscheiden sich nicht. Im anderen Extremfall, wenn das Bestimmtheitsmaß 0 ist, ist die Regressionsgerade nicht dazu geeignet, einen y-Wert vorherzusagen. Informationen zur Berechnung von2 finden Sie weiter unten in diesem Thema unter "Hinweise". |
|
sey |
Der Standardfehler des Schätzwerts y (Prognosewert). |
|
F |
Die F-Statistik (oder der berechnete F-Wert). Anhand der F-Statistik können Sie entscheiden, ob die zwischen der abhängigen und der unabhängigen Variablen beobachtete Beziehung zufällig ist oder nicht. |
|
df |
Der Freiheitsgrad. Mit diesem Freiheitsgrad können Sie den jeweiligen kritischen F-Wert (Quantil F) aus einer entsprechenden statistischen Tabelle entnehmen. Vergleichen Sie den jeweils auf diese Weise ermittelten kritischen F-Wert mit der von RGP zurückgegebenen F-Statistik, um das Konfidenzniveau Ihres Modells zu beurteilen. Informationen zur Berechnung von df finden Sie unter "Hinweise". In Beispiel 4 ist die Verwendung von F und df dargestellt. |
|
ssreg |
Die Regressions-Quadratsumme. |
|
ssresid |
Die Residual-Quadratsumme (Summe der Abweichungsquadrate). Weitere Informationen zur Berechnung von ssreg und ssresid finden Sie unter "Hinweise". |
Die folgende Abbildung zeigt, in welcher Reihenfolge die zusätzlichen Regressionskenngrößen zurückgegeben werden.

Hinweise
-
Jede Gerade lässt sich durch ihre Steigung und die jeweilige Anfangsordinate (y-Achsenabschnitt) beschreiben:
Steigung (m):
Um die Steigung einer Linie zu finden, die häufig als m geschrieben wird, nehmen Sie zwei Punkte auf der Linie, (x1,y1) und (x2,y2); Die Steigung ist gleich (y2 - y1)/(x2 - x1).Y-Intercept (b):
Der y-Abschnitt einer Linie, die häufig als b geschrieben wird, ist der Wert von y an dem Punkt, an dem die Linie die y-Achse kreuzt.Eine Gerade wird durch die Gleichung y = mx + b beschrieben. Sobald Ihnen die Werte von m und b bekannt sind, können Sie alle Punkte der Geraden berechnen, indem Sie den jeweiligen y- oder x-Wert in die Gleichung einsetzen. Sie können dafür auch die TREND-Funktion verwenden.
-
Wenn nur eine unabhängige x-Variable vorliegt, können Sie die Steigung und den y-Achsenabschnitt direkt mithilfe der folgenden Formeln ermitteln:
Steigung:
=INDEX(LINEST(known_y's;known_x's);1)Y-Intercept:
=INDEX(LINEST(known_y;known_x's);2) -
Die Genauigkeit einer von der RGP-Funktion berechneten Geraden hängt davon ab, wie sehr die betreffenden Daten gestreut sind. Je linearer sich die Daten verhalten, desto genauer ist das von RGP ermittelte Modell. RGP verwendet die Methode der kleinsten Quadrate, um die für die jeweiligen Daten beste Anpassung zu ermitteln. Wenn nur eine unabhängige x-Variable vorliegt, werden m und b entsprechend der folgenden Formeln berechnet:
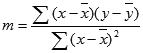
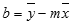
wobei x und y Beispielmöglichkeiten darstellen, d. h. x = MITTELWERT(X_Werte) und y = MITTELWERT(Y_Werte).
-
Die Regressionsfunktionen RGP (lineare Regression) und RKP (exponentielle Regression) können die Koeffizienten der an die von Ihnen bereitgestellten Daten optimal angepassten Geraden beziehungsweise Exponentialkurve berechnen. Sie müssen dennoch entscheiden, welches der beiden Ergebnisse Ihren Daten eher entspricht. Bei einer Geraden können Sie TREND(Y_Werte;X_Werte) und bei einer Exponentialkurve VARIATION(Y_Werte;X_Werte) berechnen. Werden diese Funktionen ohne das Argument Neue_x_Werte verwendet, geben sie eine Matrix mit y-Werten zurück, die an den x-Werten Ihrer tatsächlichen Datenpunkte als Vorhersagewerte auf der Geraden oder Exponentialkurve liegen. Diese Vorhersagewerte können Sie mit den tatsächlichen Werten vergleichen. Um eine bessere Vergleichsmöglichkeit zu haben, kann es sinnvoll sein, die Werte in Diagrammen darzustellen.
-
Bei der Regressionsanalyse berechnet Excel für jeden Punkt das Quadrat der Differenz zwischen dem für diesen Punkt erwarteten y-Wert und dem entsprechenden tatsächlichen y-Wert. Die Summe dieser quadrierten Differenzen wird als Residual-Quadratsumme (ssresid) bezeichnet. Anschließend berechnet Excel die Gesamtsumme der Abweichungsquadrate (sstotal). Ist das Argument Konstante mit WAHR belegt oder nicht angegeben, entspricht die Gesamtsumme der Abweichungsquadrate der Summe der quadratischen Differenzen zwischen den tatsächlichen y-Werten und dem Mittelwert der y-Werte. Wenn das Argument Konstante mit FALSCH belegt ist, entspricht die Gesamtsumme der Abweichungsquadrate den Quadraten der tatsächlichen y-Werte (ohne Subtraktion der Mittelwerte aller y-Werte von jedem einzelnen y-Wert). Anschließend kann die Regressions-Quadratsumme (ssreg) anhand der folgenden Gleichung berechnet werden: ssreg = sstotal - ssresid. Je kleiner die Restsumme der Quadrate im Vergleich zur Gesamtsumme der Quadrate ist, desto größer ist der Wert des Bestimmungskoeffizientenr2, der ein Indikator dafür ist, wie gut die aus der Regressionsanalyse resultierende Gleichung die Beziehung zwischen den Variablen erklärt. Der Wert von r2 entspricht ssreg/sstotal.
-
In einigen Fällen kann eine oder mehrere der X-Spalten (davon ausgehen, dass Y- und X-Spalten in Spalten enthalten sind) möglicherweise keinen zusätzlichen Vorhersagewert im Vorhandensein der anderen X-Spalten aufweisen. Anders ausgedrückt: Das Entfernen einer oder mehrerer X-Spalten kann zu vorhergesagten Y-Werten führen, die genauso genau sind. In diesem Fall sollten diese redundanten X-Spalten aus dem Regressionsmodell weggelassen werden. Dieses Phänomen wird als "Kollinearität" bezeichnet, da jede redundante X-Spalte als Summe von Vielfachen der nicht redundanten X-Spalten ausgedrückt werden kann. Die LINEST-Funktion überprüft die Kollinearität und entfernt alle redundanten X-Spalten aus dem Regressionsmodell, wenn sie identifiziert werden. Entfernte X-Spalten können in der LINEST-Ausgabe als 0 Koeffizienten zusätzlich zu 0 se-Werten erkannt werden. Wenn eine oder mehrere Spalten als redundant entfernt werden, ist df betroffen, da df von der Anzahl der X-Spalten abhängt, die tatsächlich für Vorhersagezwecke verwendet werden. Ausführliche Informationen zur Berechnung von df finden Sie unter Beispiel 4. Wenn df geändert wird, weil redundante X-Spalten entfernt werden, sind auch die Werte sey und F betroffen. Kollinearität sollte in der Praxis relativ selten sein. Ein Fall, in dem die Wahrscheinlichkeit höher ist, ist jedoch, wenn einige X-Spalten nur 0- und 1-Werte als Indikatoren dafür enthalten, ob ein Subjekt in einem Experiment Mitglied einer bestimmten Gruppe ist oder nicht. Wenn const = TRUE oder ausgelassen wird, fügt die LINEST-Funktion effektiv eine zusätzliche X-Spalte aller 1 Werte ein, um den Intercept zu modellieren. Wenn Sie über eine Spalte mit einer 1 für jedes Thema verfügen, falls männlich, oder 0, wenn nicht, und Sie auch eine Spalte mit einer 1 für jeden Betreff haben, wenn weiblich, oder 0, wenn nicht, ist diese zweite Spalte redundant, da die Einträge darin aus dem Subtrahieren des Eintrags in der Spalte "männlicher Indikator" vom Eintrag in der zusätzlichen Spalte aller 1-Werte abgerufen werden können, die von der LINEST-Funktion hinzugefügt werden.
-
Der Wert "df" wird folgendermaßen berechnet, wenn keine X-Spalten aufgrund von Kollinearität aus dem Modell entfernt werden: Wenn k Spalten für X_Werte vorhanden sind und Konstante mit WAHR belegt oder nicht angegeben ist, gilt df = n – k – 1. Wenn Konstante mit FALSCH belegt ist, gilt df = n - k. In beiden Fällen wird der Wert "df" um die Anzahl der aufgrund von Kollinearität entfernten Spalten erhöht.
-
Wird eine Matrixkonstante (wie zum Beispiel X_Werte) als Argument eingegeben, müssen Sie Punkte verwenden, um Werte innerhalb derselben Zeile zu trennen, und Semikola, um die Zeilen zu trennen. Die Trennzeichen können je nach den Ländereinstellungen unterschiedlich sein.
-
Beachten Sie, dass mithilfe einer Regressionsgleichung vorhergesagte y-Werte sind möglicherweise ungültig, wenn diese außerhalb des Bereiches der y-Werte liegen, die Sie zur Ermittlung der Gleichung verwendet haben.
-
Der zugrunde liegende Algorithmus in der RGP-Funktion unterscheidet sich vom zugrunde liegenden Algorithmus der Funktionen STEIGUNG und ACHSENABSCHNITT. Bei unbestimmten und kollinearen Daten kann der Unterschied zwischen diesen Algorithmen zu unterschiedlichen Ergebnissen führen. Wenn beispielsweise die Datenpunkte des Arguments Y_Werte den Wert 0 und die Datenpunkte des Arguments X_Werte den Wert 1 aufweisen, geschieht Folgendes:
-
RGP gibt einen Wert 0 zurück. Der Algorithmus der Funktion RGP soll vernünftige Ergebnisse für kollineare Daten zurückgeben, und in diesem Fall wird mindestens ein Ergebnis ermittelt.
-
STEIGUNG und ACHSENABSCHNITT geben den Fehlerwert #DIV/0! zurück. Der Algorithmus der Funktionen STEIGUNG und ACHSENABSCHNITT soll ausschließlich ein einziges Ergebnis ermitteln, und in diesem Fall sind mehrere Ergebnisse möglich.
-
-
Neben der Verwendung von RKP zum Berechnen von Statistiken für andere Regressionstypen können Sie RGP zum Berechnen eines Bereichs von Regressionstypen verwenden, indem Sie Funktionen der x- und y-Variablen als x- und y-Reihen für RGP eingeben. Beispielsweise wird die folgende Formel:
=RGP(Y_Werte; X_Werte^SPALTE($A:$C))
verwendet, wenn Sie über eine Spalte von y-Werten und eine Spalte von x-Werte verfügen, um die kubische (Polynom der Ordnung 3) Annäherung in folgender Form zu berechnen:
y = m1*x + m2*x^2 + m3*x^3 + b
Sie können diese Formel anpassen, um andere Regressionstypen zu berechnen. In einigen Fällen ist dafür die Anpassung der Ausgabewerte und anderer Statistiken erforderlich.
-
Der von der LINEST-Funktion zurückgegebene F-Test-Wert unterscheidet sich vom F-Test-Wert, der von der FTEST-Funktion zurückgegeben wird. LINEST gibt die F-Statistik zurück, während FTEST die Wahrscheinlichkeit zurückgibt.
Beispiele
Beispiel 1: Steigung und y-Achsenabschnitt
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Y-Wert |
x-Wert |
|---|---|
|
1 |
0 |
|
9 |
4 |
|
5 |
2 |
|
7 |
3 |
|
Ergebnis (Steigung) |
Ergebnis (y-Achsenabschnitt) |
|
2 |
1 |
|
Formel (Matrixformel in Zellen A7:B7) |
|
|
=RGP(A2:A5;B2:B5;;FALSCH) |
Beispiel 2: Einfache lineare Regression
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Monat |
Umsatz |
|---|---|
|
1 |
3.100 € |
|
2 |
4.500 € |
|
3 |
4.400 € |
|
4 |
5.400 € |
|
5 |
7.500 € |
|
6 |
8.100 € |
|
Formel |
Ergebnis |
|
=SUMME(RGP(B1:B6;A1:A6)*{9.1}) |
11.000 € |
|
Berechnet den geschätzten Umsatz für den neunten Monat auf Grundlage der Umsätze in den Monaten 1 bis 6. |
Beispiel 3: Multiple lineare Regression
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Grundfläche (x1) |
Büroräume (x2) |
Eingänge (x3) |
Alter (x4) |
Schätzwert (y) |
|---|---|---|---|---|
|
2310 |
2 |
2 |
20 |
142.000 € |
|
2333 |
2 |
2 |
12 |
144.000 € |
|
2356 |
3 |
1,5 |
33 |
151.000 € |
|
2379 |
3 |
2 |
43 |
150.000 € |
|
2402 |
2 |
3 |
53 |
139.000 € |
|
2425 |
4 |
2 |
23 |
169.000 € |
|
2448 |
2 |
1,5 |
99 |
126.000 € |
|
2471 |
2 |
2 |
34 |
142.900 € |
|
2494 |
3 |
3 |
23 |
163.000 € |
|
2517 |
4 |
4 |
55 |
169.000 € |
|
2540 |
2 |
3 |
22 |
149.000 € |
|
-234,2371645 |
||||
|
13,26801148 |
||||
|
0,996747993 |
||||
|
459,7536742 |
||||
|
1732393319 |
||||
|
Formel (in A19 eingegebene dynamische Arrayformel) |
||||
|
=RGP(E2:E12;A2:D12;WAHR;WAHR) |
Beispiel 4: Verwenden der F- undr2-Statistik
Im vorherigen Beispiel beträgt der Bestimmungskoeffizient oderr2 0,99675 (siehe Zelle A17 in der Ausgabe für LINEST), was auf eine starke Beziehung zwischen den unabhängigen Variablen und dem Verkaufspreis hindeutet. Sie können die F-Statistik verwenden, um zu bestimmen, ob diese Ergebnisse mit einem so hohen r2-Wert zufällig aufgetreten sind.
Stellen Sie dazu die Hypothese auf, dass zwischen den Variablen eigentlich kein Zusammenhang besteht, sondern dass Sie nur zufällig eine Stichprobe von 11 Bürogebäuden erhoben haben, für die die statistische Analyse einen starken Zusammenhang anzeigt. Um die Wahrscheinlichkeit zu beschreiben, mit der irrtümlich ein Zusammenhang ermittelt wird, wird die Irrtumswahrscheinlichkeit "Alpha" verwendet.
Die F- und df-Werte in der Ausgabe der LINEST-Funktion können verwendet werden, um die Wahrscheinlichkeit zu bewerten, dass zufällig ein höherer F-Wert auftritt. F kann mit kritischen Werten in veröffentlichten F-Verteilungstabellen verglichen werden, oder die Funktion FDIST in Excel kann verwendet werden, um die Wahrscheinlichkeit zu berechnen, dass ein größerer F-Wert zufällig auftritt. Die entsprechende F-Verteilung verfügt über die Freiheitsgrade v1 und v2. Wenn n die Anzahl der Datenpunkte und const = TRUE oder ausgelassen ist, dann v1 = n – df – 1 und v2 = df. (Wenn const = FALSE, dann v1 = n – df und v2 = df.) Die FDIST-Funktion mit der Syntax FDIST(F,v1,v2) gibt die Wahrscheinlichkeit zurück, dass ein höherer F-Wert zufällig auftritt. In diesem Beispiel: df = 6 (Zelle B18) und F = 459,753674 (Zelle A18).
Angenommen, ein Alpha-Wert von 0,05, v1 = 11 – 6 – 1 = 4 und v2 = 6, ist die kritische Ebene von F 4,53. Da F = 459,753674 viel höher als 4,53 ist, ist es äußerst unwahrscheinlich, dass ein F-Wert dieser Höhe zufällig aufgetreten ist. (Bei Alpha = 0,05 ist die Hypothese, dass es keine Beziehung zwischen known_y und known_x gibt , abzulehnen, wenn F den kritischen Wert 4,53 überschreitet.) Sie können die Funktion FDIST in Excel verwenden, um die Wahrscheinlichkeit zu erhalten, dass ein F-Wert dieser Höhe zufällig aufgetreten ist. Beispiel : FDIST(459.753674, 4, 6) = 1,37E-7, eine extrem geringe Wahrscheinlichkeit. Sie können entweder durch Ermitteln der kritischen Ebene von F in einer Tabelle oder mithilfe der Funktion FDIST schlussfolgern, dass die Regressionsgleichung nützlich ist, um den bewerteten Wert von Bürogebäuden in diesem Bereich vorherzusagen. Denken Sie daran, dass es wichtig ist, die richtigen Werte von v1 und v2 zu verwenden, die im vorherigen Absatz berechnet wurden.
Beispiel 5: Berechnen der t-Statistik
Mithilfe einer anderen Hypothese kann festgestellt werden, ob die einzelnen Steigungskoeffizienten geeignet sind, den Schätzwert eines der in Beispiel 3 aufgeführten Bürogebäude zu berechnen. Um zum Beispiel den Koeffizienten für das Gebäudealter bezüglich der statistischen Wahrscheinlichkeit (Sicherheit) zu prüfen, dividieren Sie –234,24 (Steigungskoeffizient für das Alter) durch 13,268 (der in Zelle 15 stehende Standardfehler des Alterskoeffizienten). Daraus ergibt sich der folgende t-Wert:
t = m4 ÷ se4 = -234,24 ÷ 13,268 = -17,7
Wenn der Absolutwert von t hoch genug ist, kann geschlussfolgert werden, dass der Steigungskoeffizient für die Berechnung des bewerteten Werts eines Bürogebäudes in Beispiel 3 hilfreich ist. In der folgenden Tabelle sind die Absolutwerte der vier berechneten t-Werte dargestellt.
Wenn Sie die entsprechende Tabelle eines Statistikhandbuchs zu Rate ziehen, werden Sie feststellen, dass der kritische t-Wert bei einem zweiseitigen Test mit sechs Freiheitsgraden und Alpha = 0,05 den Wert 2,447 hat. Dieser kritische Wert kann auch mithilfe der TINV-Funktion in Excel ermittelt werden. TINV(0,05.6) = 2,447. Da der Absolutwert von t (17,7) größer als 2,447 ist, ist Alter eine zuverlässige Variable, um den Schätzwert eines Bürogebäudes zu ermitteln. Für alle weiteren unabhängigen Variablen kann die statistische Wahrscheinlichkeit auf dieselbe Weise geprüft werden. Für die anderen unabhängigen Variablen werden die folgenden t-Werte ermittelt:
|
Variable |
Berechneter t-Wert |
|---|---|
|
Grundfläche |
5,1 |
|
Anzahl der Büros |
31,3 |
|
Anzahl der Eingänge |
4,8 |
|
Alter |
17,7 |
Alle Werte haben einen Absolutwert, der größer als 2,447 ist. Daher sind alle Variablen, die in der Regressionsgleichung verwendet werden, geeignet, den Schätzwert eines zum fraglichen Büroviertel gehörenden Bürogebäudes zu bestimmen.










