In diesem Artikel werden die Formelsyntax und die Verwendung von CONFIDENCE beschrieben. -Funktion in Microsoft Excel.
Beschreibung
Ermöglicht die Berechnung des 1-Alpha Konfidenzintervalls für den Erwartungswert einer Zufallsvariablen und verwendet dazu die Normalverteilung.
Das Konfidenzintervall ist ein Wertebereich. Ihr Stichprobenmittelwert x befindet sich in der Mitte dieses Bereichs, und der Bereich ist x ± KONFIDENZ. Wenn z. B. x der Stichprobenmittelwert der Lieferzeiten für Produkte ist, die über die Post bestellt wurden, ist x ± KONFIDENZ ein Bereich der Bevölkerung. Bei jedem Populationsmittel μ0 in diesem Bereich ist die Wahrscheinlichkeit, einen Probenmittelwert zu erhalten, der weiter von μ0 als x liegt, größer als alpha; für jeden Populationsmittelwert μ0, der sich nicht in diesem Bereich befindet, ist die Wahrscheinlichkeit, einen Stichprobenmittelwert zu erhalten, der weiter von μ0 als x liegt, kleiner als alpha. Anders ausgedrückt: Angenommen, wir verwenden x, standard_dev und size, um einen zweiseitigen Test auf Signifikanzebene alpha der Hypothese zu erstellen, dass der Grundgesamtheitsmittel μ0 ist. Dann werden wir diese Hypothese nicht ablehnen, wenn μ0 im Konfidenzintervall liegt, und diese Hypothese wird abgelehnt, wenn μ0 nicht im Konfidenzintervall liegt. Das Konfidenzintervall lässt nicht zu, dass die Wahrscheinlichkeit 1 – Alpha besteht, dass das nächste Paket eine Lieferzeit im Konfidenzintervall nimmt.
Wichtig: Diese Funktion wurde durch eine oder mehrere neue Funktionen ersetzt, die ggf. eine höhere Genauigkeit bieten und deren Namen die Verwendung besser wiedergeben. Obwohl diese Funktion aus Gründen der Abwärtskompatibilität weiterhin verfügbar ist, sollten Sie von nun an die neuen Funktionen verwenden, da die alte Funktion in zukünftigen Versionen von Excel möglicherweise nicht mehr verfügbar sein wird.
Weitere Informationen zu den neuen Funktionen finden Sie unter KONFIDENZ.NORM (Funktion) und KONFIDENZ.T (Funktion).
Syntax
KONFIDENZ(Alpha;Standabwn;Umfang)
Die Syntax der Funktion KONFIDENZ weist die folgenden Argumente auf:
-
Alpha Erforderlich. Die Irrtumswahrscheinlichkeit bei der Berechnung des Konfidenzintervalls. Das Konfidenzintervall ist gleich 100*(1 - Alpha)%, was bedeutet, dass ein Wert für Alpha von 0,05 einem Konfidenzniveau von 95% entspricht.
-
Standabwn Erforderlich. Die als bekannt angenommene Standardabweichung der Grundgesamtheit.
-
Größe Erforderlich. Der Umfang der Stichprobe.
Hinweise
-
Ist eines der Argumente kein numerischer Ausdruck, gibt KONFIDENZ den Fehlerwert #WERT! zurück.
-
Ist Alpha ≤ 0 oder ≥ 1, gibt KONFIDENZ den Fehlerwert #ZAHL! zurück.
-
Ist Standabwn ≤ 0, gibt KONFIDENZ den Fehlerwert #ZAHL! zurück.
-
Ist Umfang keine ganze Zahl, wird der Dezimalanteil abgeschnitten.
-
Ist Umfang < 1, gibt KONFIDENZ den Fehlerwert #ZAHL! zurück.
-
Wenn wir davon ausgehen, dass Alpha gleich 0,05 ist, müssen wir den Bereich unter der Standardnormalkurve berechnen, die (1 - Alpha) oder 95 Prozent entspricht. Dieser Wert ist ± 1,96. Das Konfidenzintervall lautet daher:
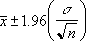
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Um die Ergebnisse der Formeln anzuzeigen, markieren Sie sie, drücken Sie F2 und dann die EINGABETASTE. Im Bedarfsfall können Sie die Breite der Spalten anpassen, damit alle Daten angezeigt werden.
|
Daten |
Beschreibung |
|
|
0,05 |
Irrtumswahrscheinlichkeit |
|
|
2,5 |
Standardabweichung der Grundgesamtheit |
|
|
50 |
Umfang der Stichprobe |
|
|
Formel |
Beschreibung |
Ergebnis |
|
=KONFIDENZ(A2;A3;A4) |
1-Alpha Konfidenzintervall für den Erwartungswert einer Zufallsvariablen. Dies bedeutet, dass das Konfidenzintervall für den zugrunde liegenden Erwartungswert einer Zufallsvariablen einer mittleren Fahrzeit zur Arbeit von 30 Minuten ± 0,692952 Minuten entspricht, also zwischen 29,3 und 30,7 Minuten. |
0,692951912 |










