Hinweis: Wir möchten Ihnen die aktuellsten Hilfeinhalte so schnell wie möglich in Ihrer eigenen Sprache bereitstellen. Diese Seite wurde automatisiert übersetzt und kann Grammatikfehler oder Ungenauigkeiten enthalten. Unser Ziel ist es, Ihnen hilfreiche Inhalte bereitzustellen. Teilen Sie uns bitte über den Link am unteren Rand dieser Seite mit, ob die Informationen für Sie hilfreich sind. Hier finden Sie den englischen Artikel als Referenz.
Ermöglicht die Berechnung des 1-Alpha Konfidenzintervalls für den Erwartungswert einer Zufallsvariable bei Normalverteilung. Ein Konfidenzintervall ist ein Bereich, der sich links und rechts des jeweiligen Stichprobenmittels erstreckt. Beispielsweise können Sie für eine Ware, die Sie per Post zugestellt bekommen, mit einer bestimmten Sicherheit (Konfidenzniveau) vorhersagen, wann sie frühestens bzw. spätestens bei Ihnen eintrifft.
Syntax
KONFIDENZ(Alpha;Standabwn;Umfang)
Alpha ist die Irrtumswahrscheinlichkeit bei der Berechnung des Konfidenzintervalls. Das Konfidenzintervall ist gleich 100*(1 - Alpha)%, was bedeutet, dass ein Wert für Alpha von 0,05 einem Konfidenzniveau von 95% entspricht.
StandardAbweichung ist die als bekannt angenommene Standardabweichung der Grundgesamtheit.
Umfang ist der Umfang der Stichprobe.
Hinweise
-
Ist eines der Argumente nicht numerisch, gibt KONFIDENZ den Fehlerwert #WERT! zurück.
-
Ist Alpha ≤ 0 oder alpha ≥ 1, gibt KONFIDENZ den #NUM #zahl! Fehlerwert.
-
Ist Standabwn ≤ 0, gibt KONFIDENZ den #NUM #zahl! Fehlerwert.
-
Ist Umfang keine ganze Zahl, wird der Dezimalanteil abgeschnitten.
-
Ist Umfang_S < 1, gibt KONFIDENZ den #NUM #zahl! Fehlerwert.
-
Ist Alpha gleich 0,05, dann muss die Fläche unter der Kurve der standardisierten Normalverteilung berechnet werden, die dem Wert (1 - Alpha) bzw. 95% entspricht. Dieser Wert ist ± 1,96. Für das Konfidenzintervall gilt daher:
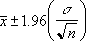
Beispiel
Angenommen, eine Stichprobe bei 50 Berufspendlern ergibt, dass diese durchschnittlich 30 Minuten benötigen, um zu ihrem Arbeitsplatz zu gelangen, wobei die Standardabweichung der Grundgesamtheit 2,5 beträgt. Dann gilt mit einer Wahrscheinlichkeit von mindestens 95 %, dass der Mittelwert der Grundgesamtheit im folgenden Intervall liegt:
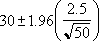
|
Alpha |
Standardabweichung |
Umfang |
Formel |
Beschreibung (Ergebnis) |
|
0,05 |
0,5 |
50 |
=KONFIDENZ([Alpha];[Standabwn];[Umfang_S]) |
1-Alpha Konfidenzintervall für den Erwartungswert einer Zufallsvariablen. Dies bedeutet eine durchschnittliche Fahrzeit zur Arbeit von 30 ± 0,692951 Minuten, also zwischen 29,3 und 30,7 Minuten. (0,692951) |










