Lineær
Beregner tilpasningen af de mindste kvadrater for en linje, der er repræsenteret af følgende ligning:
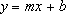
hvor m er hældningen, og b er skæringen.
Polynomisk
Beregner tilpasningen af de mindste kvadrater gennem punkter ved hjælp af følgende ligning:
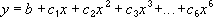
hvor b og 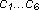
Logaritmisk
Beregner tilpasningen af de mindste kvadrater gennem punkter ved hjælp af følgende ligning:
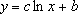
hvor c og b er konstanter, og ln er den naturlige logaritmefunktion.
Eksponentiel
Beregner tilpasningen af de mindste kvadrater gennem punkter ved hjælp af følgende ligning:
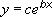
hvor c og b er konstanter, og e er den naturlige logaritmes grundtal.
Tænd/sluk
Beregner tilpasningen af de mindste kvadrater gennem punkter ved hjælp af følgende ligning:
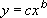
hvor c og b er konstanter.
R-kvadreret værdi
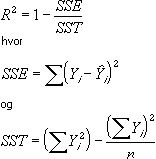
Bemærk!: Den R-kvadrerede værdi, du kan vise med en tendenslinje, er ikke en justeret R-kvadreret værdi. Til logaritmiske, potens- og eksponentielle tendenslinjer bruger Microsoft Graph en transformeret regressionsmodel.
Glidende gennemsnit
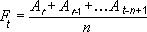
Bemærk!: Antallet af punkter i en tendenslinje med glidende gennemsnit er lig med det samlede antal punkter i serien minus det tal, du angiver for perioden.










