Bemærk!: Vi vil gerne give dig den mest opdaterede hjælp, så hurtigt vi kan, på dit eget sprog. Denne side er oversat ved hjælp af automatisering og kan indeholde grammatiske fejl og unøjagtigheder. Det er vores hensigt, at dette indhold skal være nyttigt for dig. Vil du fortælle os, om oplysningerne var nyttige for dig, nederst på denne side? Her er artiklen på engelsk så du kan sammenligne.
Returnerer konfidensintervallet for middelværdien i en population med normalfordeling. Konfidensintervallet er et interval på hver side af en eksempelmiddelværdi. Hvis du f.eks. bestiller en vare pr. postordre, kan du med en bestemt grad af sikkerhed fastsætte den tidligste og seneste modtagelsesdato for varen.
Syntaks
KONFIDENSINTERVAL(alpha;standardafv;størrelse)
Alpha er signifikansniveauet, der bruges til at beregne konfidensniveauet. Konfidensniveauet er lig med 100(1 - alpha)%, dvs. en alphaværdi på 0,05 angiver et konfidensniveau på 95%.
Standardafv er populationens standardafvigelse for dataområdet og antages at være kendt.
Størrelse er stikprøvens størrelse.
Bemærkninger
-
Hvis et argument er ikke-numerisk, returnerer KONFIDENSINTERVAL fejlværdien #VÆRDI!.
-
Hvis alpha ≤ 0 eller alpha ≥ 1, returnerer KONFIDENSINTERVAL fejlværdien #NUM!.
-
Hvis standardafv ≤ 0, returnerer KONFIDENSINTERVAL fejlværdien #NUM!.
-
Hvis størrelse ikke er et heltal, afkortes det.
-
Hvis størrelse < 1, returnerer KONFIDENSINTERVAL fejlværdien #NUM!.
-
Hvis det forudsættes, at alpha er lig med 0,05, skal det område under den normale standardkurve, der er lig med (1 - alpha) eller 95%, beregnes. Denne værdi er ± 1,96. Konfidensniveauet er derfor:
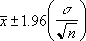
Eksempel
Lad os antage, at der i en stikprøve, som omfatter 50 rejsende, observeres en gennemsnitlig transporttid til arbejde på 30 minutter med en standardafvigelse for populationen på 2,5. Vi kan være 95% sikre på, at populationsgennemsnittet ligger inden for intervallet:
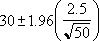
|
Alfa |
StdAfv |
Størrelse |
Formel |
Beskrivelse (resultat) |
|
0,05 |
0,5 |
50 |
=KONFIDENSINTERVAL([Alfa];[StdAfv];[Størrelse]) |
Konfidensinterval for et populationsgennemsnit. Med andre ord er den gennemsnitlige transporttid til arbejde lig med 30 ± 0,692951 minutter eller mellem 29,3 og 30,7 minutter. (0,692951) |










